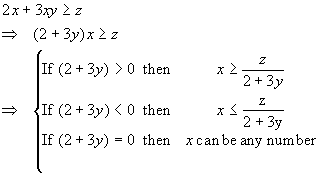ALGEBRA
Areas of focus:
- Expanding and factoring terms
- Solving an equation for an unknown
- Quadratic and biquadratic equations
- Logarithms and Exponents
- Determinants
- Systems of linear equations
- Solving linear systems in terms unknown variables
- Inequalities
Expanding
and factoring terms:
The basic rules used for reorganization of terms in an expression are
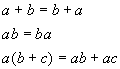
The following relations are useful in either expanding or factoring simple algebraic expressions.
![]()
![]()
![]()
![]()
x2 + Ax + B = (x + a)(x + b), where A = a + b, B = ab
![]()
Solving an
equation for an unknown:
The four basic operation of reorganization, regrouping, multiplication by a common factor, and division by a common factor can be used to solve for a unknown variable in an equation
Reorganization:
Reorganization is the process of moving the terms separated by addition, subtraction, or equality signs. When reorganization moves a term from one side of an equality to another, then the sing of the term must be changed. The following is a simple example of reorganization. All the equations convey the same information.
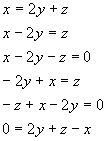
Regrouping:
The process of regrouping involves the gathering of term with common factors together. This process frequently involves reorganization, expansion of term and factoring of common expressions. The following is a simple example of regrouping of terms.
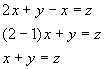
Another example of regrouping is
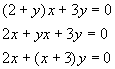
Multiplication by a common factor:
One can multiply all terms in an equation by a common factor. The resulting equation retains the relation between the variables if the factor is not zero or infinity. A simple example of multiplication by a common factor is given by
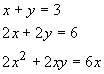
Division by a common factor:
One can divide all terms in an equation by a common factor. The resulting equation retains the relation between the variables if the factor is not zero or infinity. A simple example of division by a common factor is given by
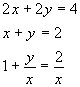
Solving for a variable:
The process of solving for a variable combines the above operations to find the value of a given variable in terms of the other variables in an equation. For example, the value of x in the following equation can be found by these steps:
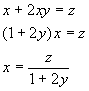
Solving for y in terms of x and z in this same equation can be done through the following steps.
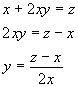
Quadratic and
bi-quadratic equations:
The quadratic equation is given by the equation ax2 + bx + c = 0,
where x is the variable to be solved for and a, b, and c
are coefficients that do not depend on x. The solution to the quadratic
equation is known as its roots and can be evaluated by
![]()
The roots of the quadratic equation are real numbers only when b2-4ac is positive or zero.
The bi-quadratic equation is ax4 + bx2 + c = 0, and has the roots
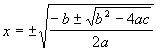
Logarithms and exponents are related by the following relation:
![]()
Where a is the base of the logarithm. If a = e = 2.718282 then the logarithm is known as the natural log, and if a = 10 it is known as the common log. The natural log of x is also written as ln(x).
Some properties of the logarithm that hold for all bases are
log (xy) = log (x) + log (y)
log (x/y) = log (x) - log (y)
log (xn )= n log (x)
Some common values of the logarithm are
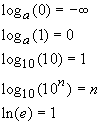
The argument of a logarithm can only be positive. The value of the logarithm is negative for arguments between zero and one, and positive for arguments grater than one (i.e., log(1) = 0, log (x) > 0 if x > 1; log (x) < 0 if 0 < x < 1).
One can use these relations to help solve equations containing exponents and logarithms. For example, one can solve for x by following the steps:
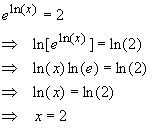
The determinant of a two by two matrix is given by
![]()
The determinant of a three by three matrix is given by
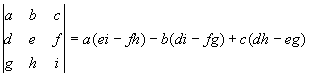
A system of linear equations is a set of two or more equations that are linear in the designated variables. An example of a system of two linear equations in the variables x and y is
![]()
One can solve a system of linear equations in terms of the designated variables by one of several different methods.
Elimination and back substitution:
The most systematic method of solving a system of linear equations is by elimination and back substitution. This involves elimination of one equation by taking one equation and solving for one variable in terms of the other variables and then substituting this expression into the remaining equations to reduce the number of equations and unknown variables. Once the system is reduced to one equation and one variable, back substitution is used to solve for the previously eliminated unknown variables. For example, for the system of equations
![]()
one can solve for x from the first equation to get
![]()
Substitution into the second equation gives one equation in y that is
![]()
This can be solved for y to get
![]()
Substitution of y back into (c) gives x as
![]()
Other methods of elimination:
One can frequently find shortcuts to solving systems of equations by adding or subtracting a multiple of one equation to the another equation. For example, the first equation in the system of equations given by
![]()
can be multiplied by 2 to get the new, but equivalent, system
![]()
Subtraction of the second equation from the first eliminates x to give
![]()
This can be solved for y to get
![]()
Any one of the above equations can now be used to get x. Substitution into the second of the original equations gives
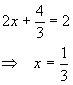
Cramer's rule:
Cramer's rule can be used to solve a linear system of equations. For example, consider the linear system
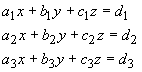
The solution to this system is
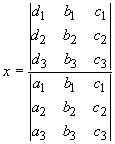
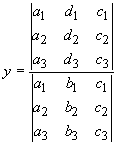
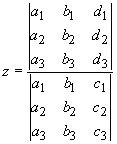
As can be seen, the solution of each unknown is the ratio of two determinants. The denominator consists of the determinant of the coefficients. The numerator consists of the determinant of a matrix that is constructed from the matrix of coefficients by replacing one column by the column of constants from the right-hand-side of the system of equations. For the first unknown, the first column of the matrix of coefficients is replaced. For the second unknown, the second column of the matrix of coefficients is replaced, and so on.
Cramer's rule can be used for any size system. If the determinant of the coefficients is zero (the system is singular), then the system cannot be inverted and does not have a unique solution. A system for which the right hand side is zero for all the equations is called homogeneous and has a nonzero solution only when the matrix of coefficients is singular.
Solving linear
systems in terms of unknown variables:
Sometimes one needs to solve a system of equations in terms of a set of unknown parameters. For example, consider the following system of equations.
![]()
This system is linear in x and y. One can solve for x and y in terms of z by simply manipulating the equations as if z was another constant. For example, elimination of x to solve for y in terms of z will involve the following steps:
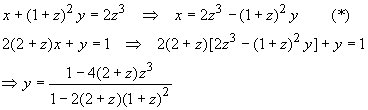
Back substitution of y into (*) gives x in terms of z.
Inequalities are manipulated in a similar manner to equalities with one exception. The direction of the inequality changes every time the equation is multiplied by a negative number. For example, consider the inequality
![]()
If both sides of the inequality are multiplied by -1, then we obviously get
![]()
As another example, consider solving for x in the inequality
![]()
The steps are