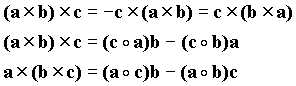VECTOR METHODS
Areas of focus:
- Vectors and vector addition
- Unit vectors
- Base vectors and vector components
- Rectangular coordinates in 2-D
- Rectangular coordinates in 3-D
- A vector connecting two points
- Dot product
- Cross product
- Triple product
- Triple vector product
A scalar is a quantity like mass or temperature that only has a magnitude.
On the other had, a vector is a mathematical object that has magnitude and
direction. A line of given length and pointing along a given direction, such as
an arrow, is the typical representation of a vector. Typical notation to
designate a vector is a boldfaced character, a character with and arrow on it,
or a character with a line under it (i.e., ![]() ). The magnitude of a vector is
its length and is normally denoted by
). The magnitude of a vector is
its length and is normally denoted by ![]() or A.
or A.
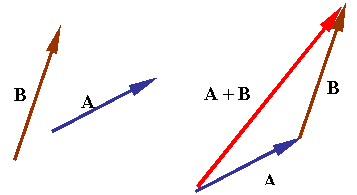
Addition of two vectors is accomplished by laying the vectors head to tail in sequence to create a triangle such as is shown in the figure.
The following rules apply in vector algebra.
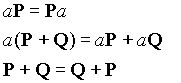
where P and Q are vectors and a is a scalar.
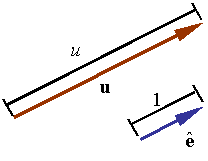
A unit vector is a vector of unit length. A unit vector is sometimes denoted
by replacing the arrow on a vector with a "^" or just adding a
"^" on a boldfaced character (i.e., ![]() ). Therefore,
). Therefore,
![]()
Any vector can be made into a unit vector by dividing it by its length.
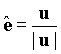
Any vector can be fully represented by providing its magnitude and a unit vector along its direction.
![]()
Base vectors and
vector components:
Base vectors are a set of vectors selected as a base to represent all other vectors. The idea is to construct each vector from the addition of vectors along the base directions. For example, the vector in the figure can be written as the sum of the three vectors u1, u2, and u3, each along the direction of one of the base vectors e1, e2, and e3, so that
![]()
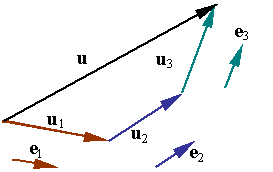
Each one of the vectors u1, u2, and u3 is parallel to one of the base vectors and can be written as scalar multiple of that base. Let u1, u2, and u3 denote these scalar multipliers such that one has
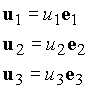
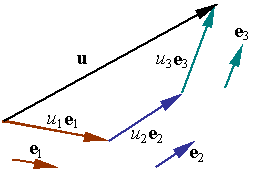
The original vector u can now be written as
![]()
The scalar multipliers u1, u2, and u3 are known as the components of u in the base described by the base vectors e1, e2, and e3. If the base vectors are unit vectors, then the components represent the lengths, respectively, of the three vectors u1, u2, and u3. If the base vectors are unit vectors and are mutually orthogonal, then the base is known as an orthonormal, Euclidean, or Cartesian base.
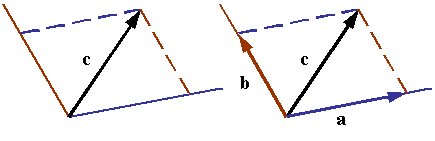
A vector can be resolved along any two directions in a plane containing it. The figure shows how the parallelogram rule is used to construct vectors a and b that add up to c.
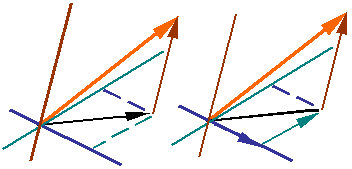
In three dimensions, a vector can be resolved along any three non-coplanar lines. The figure shows how a vector can be resolved along the three directions by first finding a vector in the plane of two of the directions and then resolving this new vector along the two directions in the plane.
When vectors are represented in terms of base vectors and components, addition of two vectors results in the addition of the components of the vectors. Therefore, if the two vectors A and B are represented by
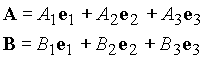
then,
![]()
Rectangular
components in 2-D:
The base vectors of a rectangular x-y coordinate system are given by
the unit vectors ![]() and
and ![]() along the x and y
directions, respectively.
along the x and y
directions, respectively.
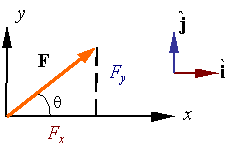
Using the base vectors, one can represent any vector F as
![]()
Due to the orthogonality of the bases, one has the following relations.
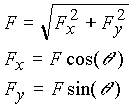
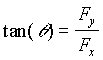
Rectangular
coordinates in 3-D:
The base vectors of a rectangular coordinate system are given by a set of
three mutually orthogonal unit vectors denoted by ![]() ,
, ![]() , and
, and ![]() that
are along the x, y, and z coordinate directions,
respectively, as shown in the figure.
that
are along the x, y, and z coordinate directions,
respectively, as shown in the figure.
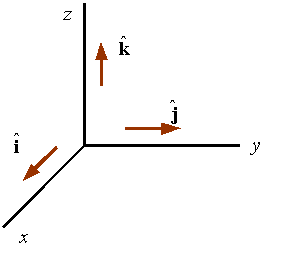
The system shown is a right-handed system since the thumb of the right hand points in the direction of z if the fingers are such that they represent a rotation around the z-axis from x to y. This system can be changed into a left-handed system by reversing the direction of any one of the coordinate lines and its associated base vector.
In a rectangular coordinate system the components of the vector are the projections of the vector along the x, y, and z directions. For example, in the figure the projections of vector A along the x, y, and z directions are given by Ax, Ay, and Az, respectively.
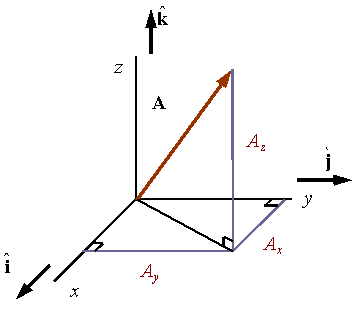
![]()
As a result of the Pythagorean theorem, and the orthogonality of the base vectors, the magnitude of a vector in a rectangular coordinate system can be calculated by
![]()
Direction cosines:
Direction cosines are defined as
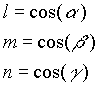
where the angles ![]() ,
, ![]() , and
, and ![]() are the
angles shown in the figure. As shown in the figure, the direction cosines
represent the cosines of the angles made between the vector and the three
coordinate directions.
are the
angles shown in the figure. As shown in the figure, the direction cosines
represent the cosines of the angles made between the vector and the three
coordinate directions.
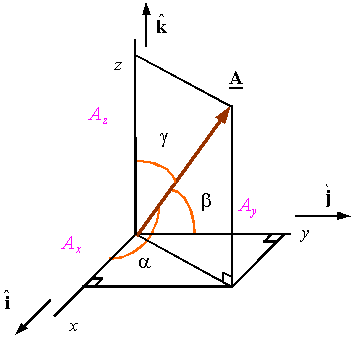
The direction cosines can be calculated from the components of the vector and its magnitude through the relations
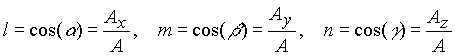
The three direction cosines are not independent and must satisfy the relation
![]()
This results form the fact that
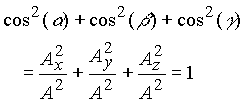
A unit vector can be constructed along a vector
using the direction cosines as its components along the x, y, and
z directions. For example, the unit-vector ![]() along the vector A
is obtained from
along the vector A
is obtained from
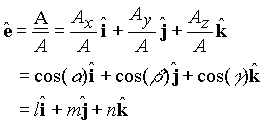
Therefore,
![]()
A vector
connecting two points:
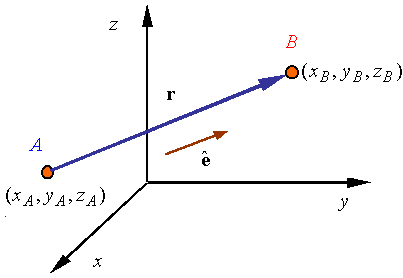
The vector connecting point A to point B is given by
![]()
A unit vector along the line A-B can be obtained from
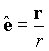
A vector F along the line A-B and of magnitude F can thus be obtained from the relation
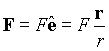
The dot product is denoted by "![]() " between two vectors. The
dot product of vectors A and B results in a scalar given by the
relation
" between two vectors. The
dot product of vectors A and B results in a scalar given by the
relation
![]()
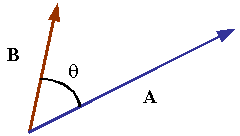
where ![]() is the angle between the two vectors. Order is not important in
the dot product as can be seen by the dot products definition. As a result one
gets
is the angle between the two vectors. Order is not important in
the dot product as can be seen by the dot products definition. As a result one
gets
![]()
The dot product has the following properties.
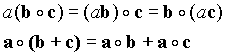
Since the cosine of 90o is zero, the dot product of two orthogonal vectors will result in zero.
Since the angle between a vector and itself is zero, and the cosine of zero is one, the magnitude of a vector can be written in terms of the dot product using the rule
![]()
Rectangular coordinates:
When working with vectors represented in a rectangular coordinate system by the components
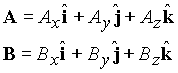
then the dot product can be evaluated from the relation
![]()
This can be verified by direct multiplication of the vectors and noting that due to the orthogonality of the base vectors of a rectangular system one has
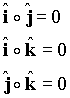
Projection of a vector onto a line:
The orthogonal projection of a vector along a line is obtained by moving one end of the vector onto the line and dropping a perpendicular onto the line from the other end of the vector. The resulting segment on the line is the vector's orthogonal projection or simply its projection.
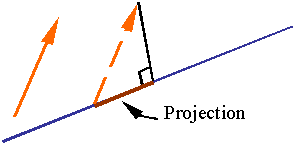
The scalar projection of vector A along the
unit vector ![]() is the length of the orthogonal projection A
along a line parallel to
is the length of the orthogonal projection A
along a line parallel to ![]() , and can be evaluated using the dot product. The
relation for the projection is
, and can be evaluated using the dot product. The
relation for the projection is
![]()
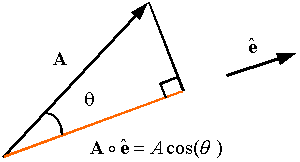
The vector projection of A along the unit
vector ![]() simply multiplies the scalar projection by the unit vector
simply multiplies the scalar projection by the unit vector ![]() to
get a vector along
to
get a vector along ![]() . This gives the relation
. This gives the relation
![]()
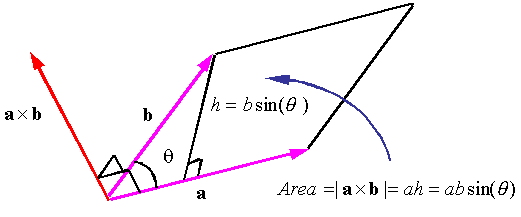
The cross product of vectors a and b is a vector perpendicular
to both a and b and has a magnitude equal to the area of the
parallelogram generated from a and b. The direction of the cross
product is given by the right-hand rule . The cross product is denoted by a
"![]() " between the vectors
" between the vectors
Order is important in the cross product. If the order of operations changes in a cross product the direction of the resulting vector is reversed. That is,
![]()
The cross product has the following properties.
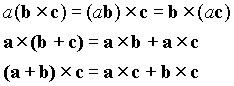
Rectangular coordinates:
When working in rectangular coordinate systems, the cross product of vectors a and b given by

can be evaluated using the rule
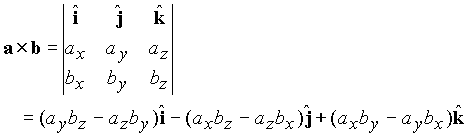
One can also use direct multiplication of the base vectors using the relations
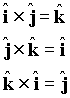

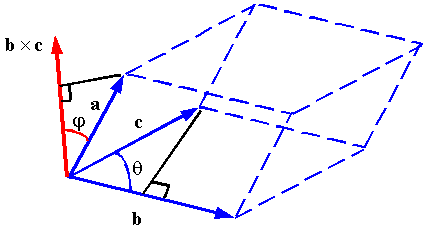
The triple product of vectors a, b, and c is given by
![]()
The value of the triple product is equal to the volume of the parallelepiped constructed from the vectors. This can be seen from the figure since

The triple product has the following properties
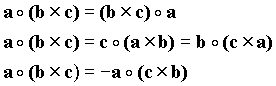
Rectangular coordinates:
Consider vectors described in a rectangular coordinate system as
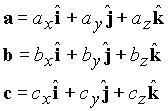
The triple product can be evaluated using the relation
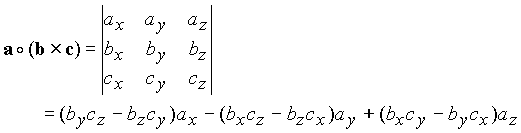
The triple vector product has the properties