Dynamics of a Golf Swing
By: Amber
Henderson
For:
Engineering Dynamics (EngM 373)
In this paper I will go through some of the dynamics involved in a golf swing. I will find the resulting velocity of the ball right after the club hits it, the distance the ball will go if you hit it exactly as I have figured, and I will also show what effects the angle of the club will have on the distance.

I will start by given all of
the information I need to proceed with the problem. I found a website
(http://homepage.Fcnetworks.net/offcampus/gift/swingweight.htm) that had the
dimensions of the club. Other
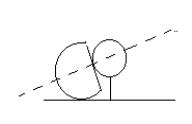
measurements were figured using the golf stance as the picture shows below and
taking measurements from that. (in units of feet, pounds, and slugs)
Club length (lclub): 3.42 ft
Club Head weight: .485 lb.
Shaft weight: .368 lb.
Loft degree (f): 10º
Plane degree (q): 72º
Angular Velocity of the club (wclub): 25.64 rad/s
Arm length (larm): 2 ft
Arm weight: 6 lb. (for both arms)
Ball weight: .125 lb.
These are the measurements I will be using throughout my project.
First I need to find the Inertia of the club, using a point on the spine of the player as a non- moving point which the club will rotate about. I will do this by the equation I=1/3ml2, which is the equation for the moment of inertia for a slender bar. I will consider the “bar” to be the club and the arms as one unit. I also need to add in the inertia of the club head to get the total inertia about the head of the player. Using the given information above, I have obtained the information I need to calculate the Inertia about the player’s head (IS ).
Mass club head (mCH)=
.485lb/32.2ft/s2 =.015 slugs
Mass of shaft (mshaft) =
.368lb/32.2ft/s2 =.011 slugs
Mass of arm (marm) =
6lb/32.2ft/s2 =.186 slugs
Length of “bar” (lbar)=larm + lclub = 2ft + 3.42ft = 5.42ft
I will use the equation
IS =1/3ml2 + ml2
With my given values to find the inertia:
IS =1/3(mshaft + marm
)lbar2 + mCH(lbar ) 2
=1/3(.011slugs +
.186slugs)(5.42ft) 2 + .015slugs(5.42ft) 2
=1.93 + .441
IS =2.37 lb*ft*s2
I will use this inertia in following equations.
Now I want to find the velocity of the ball right after the club hits it. I will do this by using the equation for the coefficient of restitution and the principle of Impulse and Momentum. The 2 equations are as follows:
1. [v*B – v*A]n
= [e(vA – vB )]n (where n is along the dotted line)
2. System Angular MomentaA
+ System Ext ImpulseA to B =
System
Angular MomentaB
Where A is the system before, B is after, and the expression A to B refers to the impulse that occurs at impact.
I will need the following data to calculate these formulas. The information is taken from above:
IH =2.37 lb*ft*s2
wclub
= 25.64 rad/s
lbar =5.42ft
Mass of the ball (mball)
= .125lb/32.2ft/s2 = .004 slugs
I also had to find the coefficient of restitution between the ball and club head material. I found this by dropping the ball on the material of a club head and finding the height of the ball before I dropped it and then the height it bounced, because the Velocity of the ball before and after was sqrt(2gh) using h before and then h* after as the determining values.
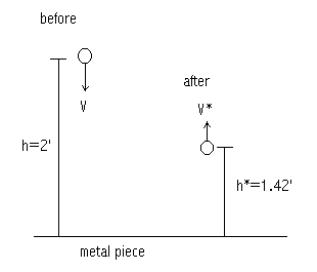
h=2ft h*=
1.42ft g= 32.2ft/s2
Using the above equation for coefficient of elasticity, I found e to be:
e=sqrt(2gh*)/sqrt(2gh)=.84
(wherever there is an asterisk ‘*’ that shows it took place after or in response to)
Now I will use the two equations 1 and 2 that I gave earlier and use them to find the velocity of the ball.
First I will start with the equation containing the coefficient of restitution.
e = velocity after/velocity before. The velocity after the impact between the ball and the clubhead is the difference of the velocity of the ball and the velocity of the club. The velocity of the ball is vball , the velocity of the club after impact is lbar(wclub)*cosf. The velocity before impact is just the velocity of the club because the ball is at rest before impact. The velocity of the club is then lbar(wclub)cosf. Therefore my equation becomes:
1. e = [vball - lbar(wclub)*cosf]/[ lbar(wclub)cosf]
Now I will derive the second equation. There is no external impulse on this system therefore System Ext ImpulseA to B =0. The System Angular momentum before impact is only due to the club, because it is the only object in motion. Therefore System Angular MomentumA= IS (wclub). The System Angular Momentum after is due to the momentum of both the club and the ball after impact. The momentum of the club after impact = IS (wclub)*, the momentum of the ball = lbar(mball)vball cosf. Therefore the equation becomes:
2. IS (wclub)
= IS (wclub)*
+ lbar(mball)vball
cosf
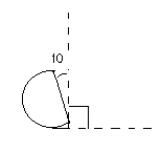
In using these two equations I have 2 equations and 2 unknowns. The two unknowns I have are Vball and wclub*. I only want to know the velocity of the ball so I will only find that one. I will use 100 degrees as f because the loft is 10° and then you have to add in 90° due to how the club lies. (refer to picture below)
2.37lb*ft*s2 (25.64 rad/s)= 2.37lb*ft*s2(wclub )* + 5.42ft(.004 slugs)(Vball)cos100
60.77=2.37wclub*
+ .018 Vball
wclub* = (60.77-.018 Vball )/2.37 (from eqn 1)
.84= [Vball – 5.42(25.64-.008 Vball )(.84)]/[5.42(25.64)(.84)]
9.81= Vball
– 116.73 + .036 Vball
214.83=1.036
Vball (from eqn 2)
Vball = 207.36 ft/s
Now that I know the magnitude of the velocity of the ball I need to find the magnitude of the velocity of the ball in the its components. I need the following information to find the velocity of the ball in its components.
f=100° (loft due to club)
q=72° (angle of the plane of swing)
Vball =207.36ft/s
![]() Y
Y
 -Z
-Z
![]()
![]() resultant velocity of ball
resultant velocity of ball
![]()
![]() a
a
![]()
 X
X
Z
The velocity in the Y direction: Vball sinfsinq =207.36(sin 100) sin 72 =194.21ft/s
The velocity in the Z direction: Vball sinfcosq = 207.36 (sin 100) cos 72=63.1ft/s
The velocity in the X direction: Vball cosf= 207.36 (cos 100)=-36ft/s
In order to find the angle a I need to find the vertical and horizontal components of the resultant velocity of the ball. The vertical component of the velocity is the velocity in the Y direction, 194.21ft/s. The horizontal component of the velocity is:
sqrt(VX2 + VZ2 )= sqrt (36.12 + 63.12)=72.65ft/s
tan a =vertical/horizontal
tan a = 194.2/72.65
a =
69.5°
Now that I know the angle at which the ball is projected I can find the distance the ball goes. I need the following given information to calculate the distance.
VO
=207.36 ft/s
a =
69.5°
First I will find the vertical components of velocity and acceleration:
(VY)O =VO sin a = 207.36 sin 69.5 = 194.2ft/s
ay = -g = -32.2 ft/s2
Using the
equation y = (VY)Ot + (1/2)at2
I can find the time it takes for the ball to hit the ground at y = 0
0 = 1.94.2t + 16.1t2
t = 12.1s
Now that I know the time the ball is in the air I can find how far it goes in the X direction. Given the following horizontal information;
(VX)O = VO cos a = 207.36 cos 69.5 = 72.6ft/s
ax = 0
Using the equation X = (VX)O t, and solving for X we find:
X
= 72.6 (12.1) = 878.46ft, or 293 yds
This answer makes sense because most drives with a driver can range from 250-325yds.
If you wanted to see the different distances achieved when changing the angles of both the plane of the swing, and the loft of the club we could try a couple of different combinations.
If we use a loft angle of 11°(they only make 9°, 10°, and 11° loft), and keep the plane degree at 72° we would get a velocity of 217 ft/s, therefore it wouldn’t go as far as a 10° loft. It would go higher in the air rather then longer. Some people would prefer the ball to go higher in the air in order to have less distance and more control. But if you want it to roll further you would have a lower loft.
If we use a plane degree of 75° ( if you stood more upright in your stance), and kept the loft at 10°, the velocity would be 214.1ft/s and it would go a shorter distance. The more you bend over in your stance the further the ball goes, that must be why whenever you get lessons they always tell you to bend over more.
In conclusion, there is a lot more than just making contact with the ball to consider when playing golf-although it’s a good start. You must take into consideration how fast you swing the club, how you stand, and the degree of loft you might consider for your type of play. I’m sure that if you talk to someone on tour he/she would have already been able to tell you everything I have just showed. To get as far as they have you have to have more knowledge than what the average golfer usually knows. I know now that the next time I’m not getting the distance I want I will take the advise of many instructors and not stand so upright, now that I have proven to myself that it is valuable advise.