CENTER PIVOT ANALYSIS

We were asked to analyze the statics involved in a real life system. I chose to evaluate a
center pivot system. In addition, I examined how the tower’s stability is affected by differing the tower’s height. The following is a description of the situation I evaluated, the calculations I made, and the results I found.
Problem: The Department of Biological Systems Engineering at the University of Nebraska-Lincoln is planning an experiment to measure the amount of carbon dioxide removed from the air by agricultural crops and the net amount of carbon that can be stored in the soil. This is part of an effort to mitigate the impact of global warming and the buildup of greenhouse gasses. Experiments will be conducted in irrigated fields. The fields that the Department will use contain center-pivot irrigation systems that have nine-feet tall towers. To conduct experiments researchers must install testing equipment that is up to 25 feet tall. The equipment will be permanently installed; therefore, the center pivot systems must be modified to provide higher clearance so that the pivot does not interfere with the testing.
My project will be to analyze the static forces involved in traditional center pivot systems that are nine-feet tall, and then analyze the change of these forces for a center pivot that is raised to a height of twenty-five feet to accommodate the University's needs. I will also analyze the stability of the different tower heights

System: Center pivots are
mechanical irrigation systems that automatically revolve in a field to apply
irrigation water through sprinklers (figure 1). The systems are typically one-quarter mile long and irrigate an
area of about 130 acres. To irrigate
tall crops the systems are designed with towers that suspend the pipe above the
ground. The minimum clearance is about
nine feet. Tires and an electric motor
are installed on the tower to propel the center pivot around the field. Steel pipe is connected between the towers
to supply water to sprinklers along the lateral. The pipe is suspended using an under-pipe truss system. The distance between towers is called a
span. The length of the span can vary
between 130 and 200 feet. The typical
pipe on the pivot has an outside diameter of 65/8 inches
with a wall thickness of 0.109 inches.
The pipe and the towers are typically galvanized to prevent
corrosion.
 Calculations: The
first step to be accomplished was to find the system’s dimensions. Lindsay Manufacturing supplied me with the
system’s dimensions. The needed
dimensions are highlighted in the dimension packet attached. There is also a dimension sheet of only the
useful dimensions. After researching
the dimensions, I began the actual calculations by calculating the weight of
the total span when the pipe is filled with water. To find this value, the weight of the water must be found as well
as the steel pipes’ weight. I began
with the free body diagram.
Calculations: The
first step to be accomplished was to find the system’s dimensions. Lindsay Manufacturing supplied me with the
system’s dimensions. The needed
dimensions are highlighted in the dimension packet attached. There is also a dimension sheet of only the
useful dimensions. After researching
the dimensions, I began the actual calculations by calculating the weight of
the total span when the pipe is filled with water. To find this value, the weight of the water must be found as well
as the steel pipes’ weight. I began
with the free body diagram.
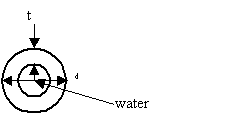
 The
first calculation I made was to find the water weight in the main pipe. Since, the pipe is 0.109” thick and 6 5/8”
in diameter, the water’s diameter is 6 5/8” – 0.109”. The volume must be found and multiplied by the density to
calculate the water’s weight.
The
first calculation I made was to find the water weight in the main pipe. Since, the pipe is 0.109” thick and 6 5/8”
in diameter, the water’s diameter is 6 5/8” – 0.109”. The volume must be found and multiplied by the density to
calculate the water’s weight.
Water Volume =
Vw = [6 5/8 – 2(0.109)]2pl/4,
where l = length of the main pipe
l can be found by using the middle truss’s dimensions. (Keep in mind, the curve of the pipe is not drawn to scale and in reality is very small.)
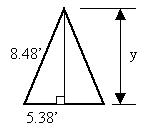

Y = [(8.48) 2+(5.38) 2]1/2 = 6.55’
Tan-1(Y/89.5) = q = 4.19 degrees
Therefore, l/2 = 89.5/cos(q) = 89.74’
Using the calculated l value in the water volume equation gives the following results.
Vw
= [6 5/8 – 2(0.109)]2p(2)(89.74)/4
= 40.18 ft3
Now, the water’s weight can be found by multiplying the volume by the density of water (1 g/cm3).
Water weight = Ww = (40.18 ft3)(1 g/cm3)(1000000 cm3/1 m3)(1 m3/(3.28)3 ft3)
Ww = 1140 kg
The next step is to calculate the weight of the steel members. The steel members fall into three categories; the main pipe, truss rods, and trusses. I began by finding the weight for each of these categories and then adding them together.
Truss Rods:
Diameter = ¾”
Volume of rods =
VR = 2[3/4]2p(89.5)(2) = 1.1 ft3
Rod weight = WR =
(1.1 ft3)(487 lb/1 ft3)(0.4536 kg/1 lb) = 243 kg
Pipe:
![]()
Diameter = 6 5/8”
Since the water fills the center of the pipe, the volume of steel is calculated by calculating the total volume and subtracting the water volume.
Pipe volume = WR = [6
5/8]2p(89.5)(2) – 40.18 =
42.97 – 40.18 = 2.79 ft3
Pipe weight = Wp = (2.79 ft3)(487 lb/1 ft3)(0.4536 kg/1 lb) = 616.32 kg
Truss:
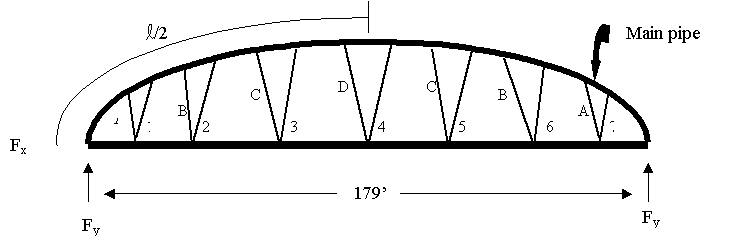
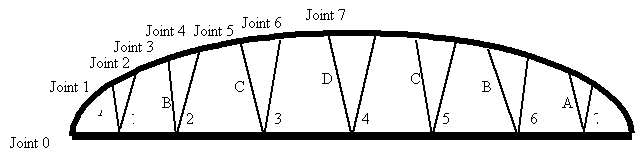
If you refer to free body diagram on page 2 the trusses are numbered 1 through 7. Due to the symmetry of the pivot system trusses 1=7, 2=6, and 3=5. The dimensions for the trusses are on the dimensions list included after the report. Following are the general equations for the volume and weight of a truss.
V = (# of braces)(width of pipe)(thickness)(length) + (width of tie)(thickness)(length)
W = (volume)(487 lb/ft3)(0.4536 kg/lb)
Trusses 1,7:
V1 = (4)(4)(3/16)(63.5) +
(3)(1/8)(62.5) = 213.94 in3 = 0.124 ft3
W1 = (0.124 ft3)(487 lb/1 ft3)(0.4536 kg/lb) = 27.39 kg
Trusses 2,6:
V2 = (4)(4)(1/8)(81.25) +
(3)(1/8)(95.125) = 0.1147 ft3
W2 = (0.1147 ft3)(487 lb/1 ft3)(0.4536 kg/lb) = 25.34 kg
Trusses 3,5:
V3 = (4)(4)(1/8)(97.75) +
(4)(1/8)(123 1/8) = 0.1488 ft3
W3 = (0.1488 ft3)(487 lb/1 ft3)(0.4536 kg/lb) = 32.87 kg
Truss 4:
V4 = (4)(4)(1/8)(101.75)
+ (3)(1/8)(129 1/8) = 0.1458 ft3
W4 = (0.1458 ft3)(487 lb/1 ft3)(0.4536 kg/lb) = 32.21 kg
Truss Totals:
WT = 2W1 + 2W2 + 2W3 + W4 = 203.41 kg
The first three truss weights are doubled, because two trusses have the same weight.
Now that each individual part of the structure has been analyzed and their weights calculated, the span’s total weight can be found. This is done by adding all the weights together.
Span Weight = SW = WW + WR + WP + WT
WS = 1140 + 243 + 616.32 + 203.41 = 2202.73 kg
The weight of the span will not change as the tower height is varied. It is important to recognize that the trusses evenly distribute the forces over the span. Therefore, by referring back to the free body diagram on page 2 Fx and Fy can be found by the summation of forces method.
SFx = 0 Therefore, Fx = 0
SFy = 0 2Fy = WS = 2202.73 kg Therefore, Fy
= 1101.37 kg = 2428.05 lb
The next part of the project is to analyze the trusses. The goal is to calculate the force for each member of the span. To simplify the situation into two dimensions, the span is vertically sliced parallel to the sides of the trusses. This is possible because of the systems symmetry. The resulting structure looks as follows.
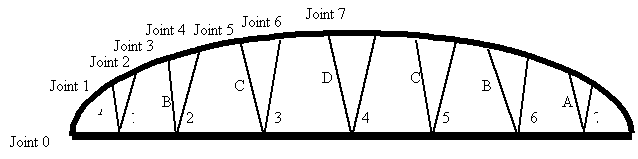 Due
to the system’s symmetry, all member forces along the bottom of the span are
equal to one another. In addition, both
braces of each truss are subjected to the same force load. To simplify the situation, the very minimal
slope from one brace to another brace within the same truss will be assumed to
be zero. To calculate the force on each
member we will begin with analyzing each joint separately.
Due
to the system’s symmetry, all member forces along the bottom of the span are
equal to one another. In addition, both
braces of each truss are subjected to the same force load. To simplify the situation, the very minimal
slope from one brace to another brace within the same truss will be assumed to
be zero. To calculate the force on each
member we will begin with analyzing each joint separately.
F0,8 F0,1
![]()
![]()
![]()
![]() Joint 0
Joint 0
Fx Fy q
![]() SFy = 0 Fy = F0,1SIN(q) F0,1
= 2428.05/SIN(13.18)
SFy = 0 Fy = F0,1SIN(q) F0,1
= 2428.05/SIN(13.18)
F0,1
= 10648,83 lb
SFx = 0 F0,1COS(q) =
F0,8
q = 13.18 degrees F0,8 = 10368.32 lb
Joint 1
63.5 a FA 13.18 F1,2 ![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
SFy = 0 F0,1SIN(q) = FACOS(13.14) FA
= 2493.33 lb
SFx = 0
a 28.875/2
F0,1 F1,2 + FASIN(13.14)
= F0,1COS(13.18)
a = 13.14 degrees F1,2 = 9801.51 lb
F2,3 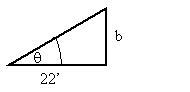
Joint
2
F1,2 FA q
![]()
![]()
![]()
![]()
![]()
![]()
![]()
SFy = 0
SFACOS(13.14) = F2,3SIN(q)
13.14
(truss
2 – 1) F2,3 =
35,426.48 lb
q = 3.93 degrees

Joint
3
14.44 q q FB 3.93 F3,4
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
SFy = 0
81.25
F2,3SIN(3.93) = FBSIN(79.76) FB
= 2467.35 lb
SFx = 0
F2,3 F2,3COS(3.93) = FBCOS(79.76) + F3,4
q = 79.76 degrees F3,4 = 34,904.55 lb
F4,5
Joint
4
F3,4 FB q
![]()
![]()
![]()
![]()
![]()
![]()
SFy = 0
SFBSIN(79.76) = F4,5SIN(q)
79.76
![]() (truss
3 – 2) F4,5 =
38,455.69 lb
(truss
3 – 2) F4,5 =
38,455.69 lb
q = 3.62 degrees

Joint
5
14.44 q q Fc 3.62 F5,6
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
SFy = 0
97.73
F4,5SIN(3.62) = FCSIN(81.50) FC =
2455.02 lb
F4,5 SFx = 0
F4,5COS(3.62) = FCCOS(81.50) + F5,6
q = 81.50 degrees F5,6 = 38,016.09 lb
F6,7
Joint 6
F5,6 q
![]()
![]()
![]()
![]()
![]()
![]()
SFy = 0
FCSIN(81.50) = F6,7SIN(q)
81.50
![]() (truss
4 – 3) F6,7 =
158,093.98 lb
(truss
4 – 3) F6,7 =
158,093.98 lb
FC
q = 0.88 degrees

Joint 7
14.44 q q FD F7
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
SFy = 0
0.88 101.75
F6,7SIN(0.88)
= FDSIN(81.84) FD
= 2452.89 lb
F6,7 SFx = 0
F6,7COS(0.88) = FDCOS(81.84) + F7
q = 81.84 degrees F7
= 157,727.18 lb
Member Forces (lbs)
F0,1 10648.83 FA 2493.33
F0,8 10368.32 FB 2467.35
F1,2 9801.51 FC 2455.02
F2,3 35426.48 FD 2452.89
F3,4 34904.55
F4,5 38455.69
F5,6 38016.09
F6,7 158093.98
F7 157727.18
The next part of the calculation process is the analysis of each tower. First, the missing dimensions for all three tower heights must be calculated. The values for each dimension in the new towers were found by using a ratio.
9/16.5 = 0.545 and 9/25 = 0.36

The dimensions for the first tower are given on the dimension sheet.
|
16.5'
Tower |
|
25'
Tower |
|
20.17' |
brace |
30.56' |
|
23.2' |
tie |
35.16' |
|
81.42" |
a |
123.26" |
|
46.33" |
b |
70.14" |
|
28.90" |
c |
43.75" |
|
88.07" |
A |
133.33" |
|
44.04" |
B |
66.67" |
|
51.38" |
C |
77.78" |
|
|
|
|
Now that the towers have been analyzed, their stability can be tested. I performed two stability tests. The first test was on how tower height affects the stability of the tower. The second test concerned the tower’s stability when the central angle is varied. To perform these tests I first had to determine the towers’ weight and the centroid of mass. The tires are approximately 75 lbs each and the motor is about 100 lbs.
9 ft Tower
brace 1:
V1 = 2(8)(1/4)(132) + (3)(1/8)(44.325) + (3)(1/8)(25.25) + (3)(1/8)(15.75)
V1 = 560 in3
W1 =
(560 in3)(487 lbs/1728 in3) = 157.83 lb
brace 2:V2 = 2(8)(1/4)(132)
V2 = 528 in3
W2 = (528 in3)(487
lbs/1728 in3) = 148.8 lb
Tie: V3 = [(6.625)2p(12.64’)(12”)]/4 = 5228.65 in3
W3 =
(5228.65 in3)(487 lbs/1728 in3) = 1473.58 lb
WT = W1 + W2 + W3 + motor + wheels
WT = 2030.21 lb
Centroid:
YWT = (4.5)W1 + (4.5)W2 = 1379.835 Therefore, Y = 0.68 ft
16.5 ft Tower
brace 1:
V1 = 2(8)(1/4)(242.04) + (3)(1/8)(81.42) + (3)(1/8)(46.33) + (3)(1/8)(28.9)
V1 = 1026.9 in3
W1 =
(1026.9 in3)(487 lbs/1728 in3) = 289.41 lb
brace 2: V2 = 2(8)(1/4)(242.04)
V2 = 968.16 in3
W2 =
(968.16 in3)(487 lbs/1728 in3) = 272.86 lb
Tie: V3 = [(6.625)2p(23.2’)(12”)]/4 = 9596.90 in3
W3 =
(9596.90 in3)(487 lbs/1728 in3) = 2704.68 lb
WT = W1 + W2 + W3 + motor + wheels
WT = 3516.95 lb
Centroid:
YWT = (8.25)W1 + (8.25)W2 = 4638.73 Therefore, Y = 1.32 ft
25 ft Tower
brace 1:
V1 = 2(8)(1/4)(366.72) + (3)(1/8)(123.26) + (3)(1/8)(70.14) + (3)(1/8)(43.75)
V1 = 1555.81 in3
W1 =
(1555.81 in3)(487 lbs/1728 in3) = 438.49 lb
brace 2: V2 = 2(8)(1/4)(366.72)
V2 = 1466.88 in3
W2 =
(1466.88 in3)(487 lbs/1728 in3) = 413.41 lb
Tie: V3 = [(6.625)2p(421.92)]/4 = 14544.26 in3
W3 = (14544.26 in3)(487
lbs/1728 in3) = 4098.99 lb
WT = W1 + W2 + W3 + motor + wheels
WT = 5200.89 lb
Centroid:
YWT = (12.5)W1 + (12.5)W2 Therefore, Y = 2.05 ft
The central angle (original) needs to be calculated. This can be done by using the dimensions of the 9 foot tower.

9’ 11’ q/2 = 35.10 degrees
q/2
Therefore,
q = 70.2 degrees
To compare the stability of the towers general formulas can be used. These general formulas are as follows.
Brace length = height/COS(q/2)
Tie length = 2(height)(TAN(q/2)
Centroid = 0.006(height)
The centroid formula was found by using the ratio found by dividing the centroid of a tower by it’s height. It turned out
that all three tower heights have the same ratio.
Centroid/height = 0.68”/9’ = 1.32”/16.5’ = 2.05”/25’ = 0.006
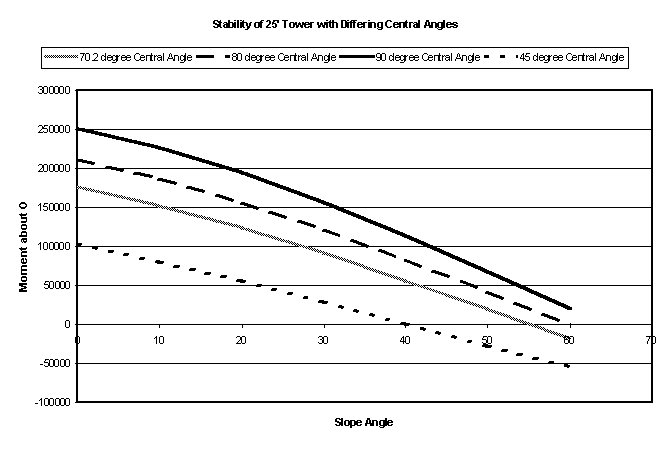
Using the general equations and a central angle of 70.2 degrees, I was able to calculate the moments about 0. This allowed me to consider the satiability of each tower. Analyzing the moment about 0, allows you to determine if the weight from the span will tip the tower over at different slope angles (negative moment). If the span weight is not great enough the system would remain standing when the slope was removed. I looked at the satiability of all three towers placed on three different slopes.
q
![]()
![]()

The general equation for the moment about 0 is as follows:
![]()
I used a spread sheet in Microsoft Excel to calculate the moments of the different heights at different slope angles and different central angles.
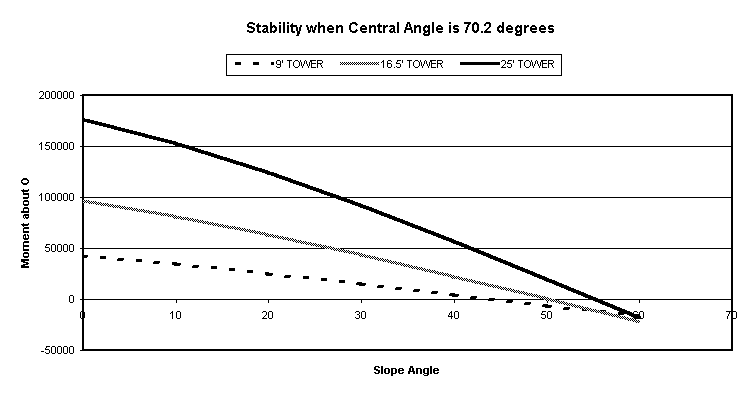
The first set of spreadsheets and graphs attached are the results from differing slope angle. The central angle was left at the constant value of 70.2 degrees during this test. The results show that the taller towers remain stable longer. The 25’ tower is stable until the slope angle approaches 65 degrees. Refer to attached charts and graphs.
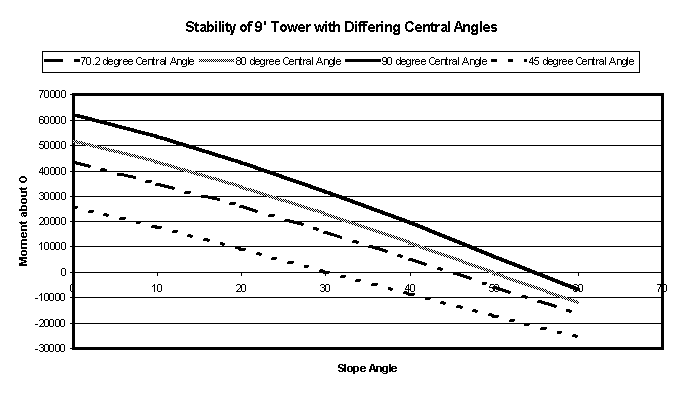
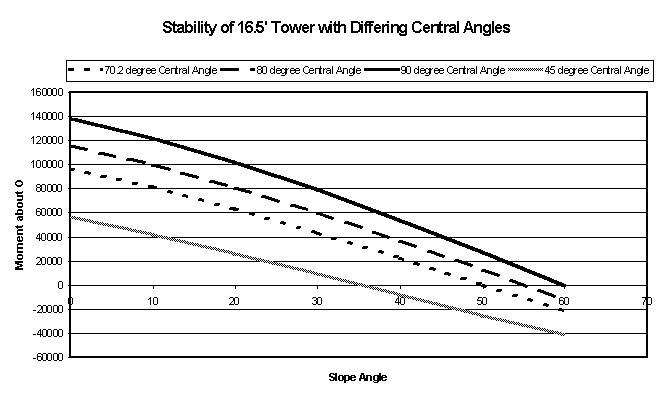
The second stability test was to observe how the stability is affected as the central angle is varied. The moment values lead to the conclusion that a larger central angle results in more stable towers. This would be expected. However, it is important to remember that a large central angle requires more steel and thus increases the cost of materials. This would be a critical factor to consider when producing center pivot systems. Graphs and charts supporting these conclusions are also attached to the report.
Conclusion: My original expected outcome was that the spans of the
pivot (i.e., the pipe, truss systems, etc.) would be the same. Thus, the changes in the force members would
be small. I thought that the forces and
weights probably would not change between the different heights. I expected the main effect to be on the
tower. Also, that the forces acting on
the tower and the reaction of the tower to those loads will vary. I was interested in how the central angle
for the tower design would affect the stability. I was not sure if it should remain the same as the shorter towers
or if the angle should be changed to provide more stability? Refer to figure 2.
In the end, the force members did not change at all from the two systems. The weight forces did change due to an increase of needed material. When considering the central angle, I found that a larger central angle results in more stability. I also looked at the stability of the different tower heights on varying slope angles. From this test I discovered that the taller towers are more stable at greater slope angles. This was surprising; I would not have expected the taller towers to be more stable.
Dimension Sheet
All dimensions where supplied by Lindsay Manufacturing
Main Pipe: diameter = 6 5/8”
Wall thickness = 0.109”
Truss Rods: diameter = ¾”
Trusses:
|
Truss |
A |
b |
c |
d |
brace(angle iron) |
tie(angle iron) |
|
1,7 |
62 1/8" |
61.84" |
28 7/8" |
63 1/2" |
2" X 2" X 3/16" |
1.5" X 1.5" X 1/8" |
|
2,6 |
95 1/8" |
79.96" |
28 7/8" |
81 1/4" |
2" X 2" X 1/8" |
1.5" X 1.5" X 1/8" |
|
3,5 |
123 1/8" |
96.68" |
28 7/8" |
97 3/4" |
2" X 2" X 1/8" |
2" X 2" X 1/8" |
|
4 |
129 1/8" |
100.72" |
28 7/8" |
101 3/4" |
2" X 2" X 1/8" |
1.5" X 1.5" X 1/8" |
B,C A c d a d C B A Down the pivot
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()


Side
view of pivot
Towers:
9’ Tower Brace length = 11’ = 132”, angle iron: 4” x 4” x ¼”
Tie length = 12.64’, 6 5/8” diameter
Brace 1:
C B A a b c
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()

 a = 44 3/8” long, 1.5” x 1.5” x 1 1/8”
angle iron
a = 44 3/8” long, 1.5” x 1.5” x 1 1/8”
angle iron
b = 25 ¼” long, 1.5” x 1.5” x 1/8” angle iron
Brace length
c = 15 ¾” long, 1.5” x 1.5” x 1.8” angle iron
A = 48”
B = 24”
C = 28”
![]()
![]()
Tie:
Tie length
Length = 12.64’

Brace 2: Note: All dimensions are
Brace length
Length = 132” based
on a “dry” system.