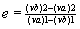
ENGM 373—Engineering Statics
Prepared Fall 2002 by Jodi Harper
Dynamics is a field that is so much a part of everyday life, many people know the results of dynamic interaction, but a much smaller percentage know why it occurs. Billiards, a pastime for over five hundred years, is one such example. It is common knowledge that the cue ball is hit, which in turn hits another ball, and both balls then move at a slower rate, and often in a different direction. While perfecting the game of billiards is something that, like any sport, takes practice, an individual with a basic knowledge of engineering mechanics can examine the game more in-depth and, at least on paper, determine the angle necessary to make a shot.
This paper will first look at collisions and compare longhand calculations with the Working Model Version 5.1.2.53 (Ó 1989-2002 MSC.Software) computer simulation. It will then show through Working Model simulation how to make a shot in billiards.
Comparison Problem
Solution Using Engineering Dynamics Calculations
This problem involves central impact. Before analyzing the mechanics of the impact, it is first necessary to obtain the velocity of the ball just before it strikes the box.
Velocity of ball prior to collision
Set the datum at q = 0 o. Using conservation of energy, we have
We know To and Vo to be equal to zero. Calculate T1 using ½ mv2 and V1 using mgr.
T1 = ½ (6/32.2) (vball)2
= 0.09317 (vball)2
V1 = - (6) (3)
= - 18
Substituting into Equation 1, we get
0 + 0 = 0.09317 (vball)2 + -18
Simplifying this, we get
0.09317 (vball)2 = 18
Solving for vball, we get
vball = 13.9 ft/s
mB(vB)1 + mA(vA)1 = mB(vB)2 + mA(vA)2 (Equation 2)
We know vb1 is zero. Substituting known values into Equation 2, we get
0 + (6/32.2) (13.9) = (18/32.2) (vb2) + (6/32.2) (va2) (Equation 3)
Since the coefficient of restitution is 0.5, we know that the balls separate after the collision. Realizing that for separation to occur, vb2 > va2, we have
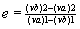
Substituting in known values, we get
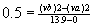
(vA)2 = -1.74 ft/s and (vB)2
=5.21 ft/s
Solution Using Working Model
To see how this scenario works, go to the Working Model Example 1.
Below are pictures from Working Model to see selected points in the
simulation.
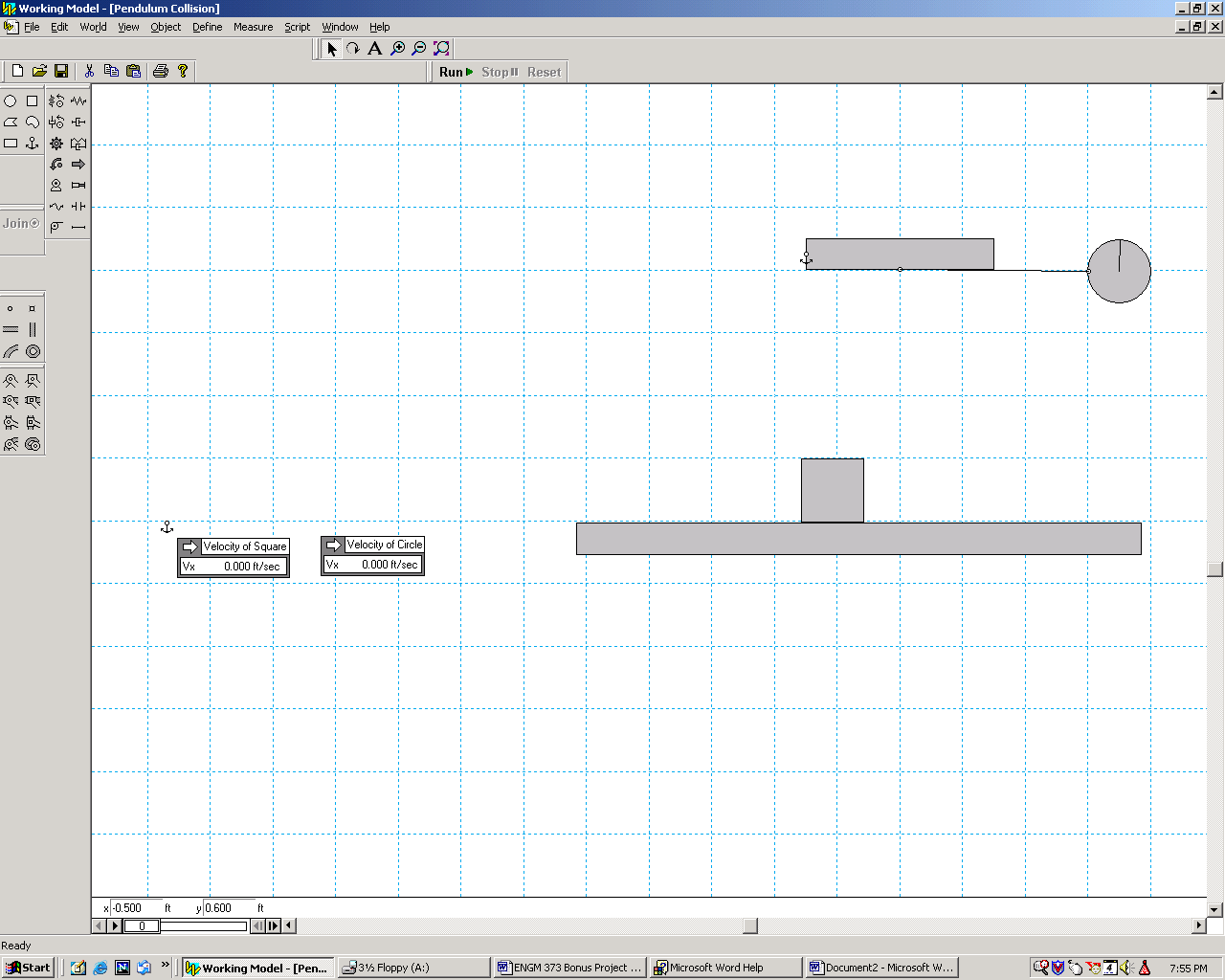
Initial starting position of ball and box.
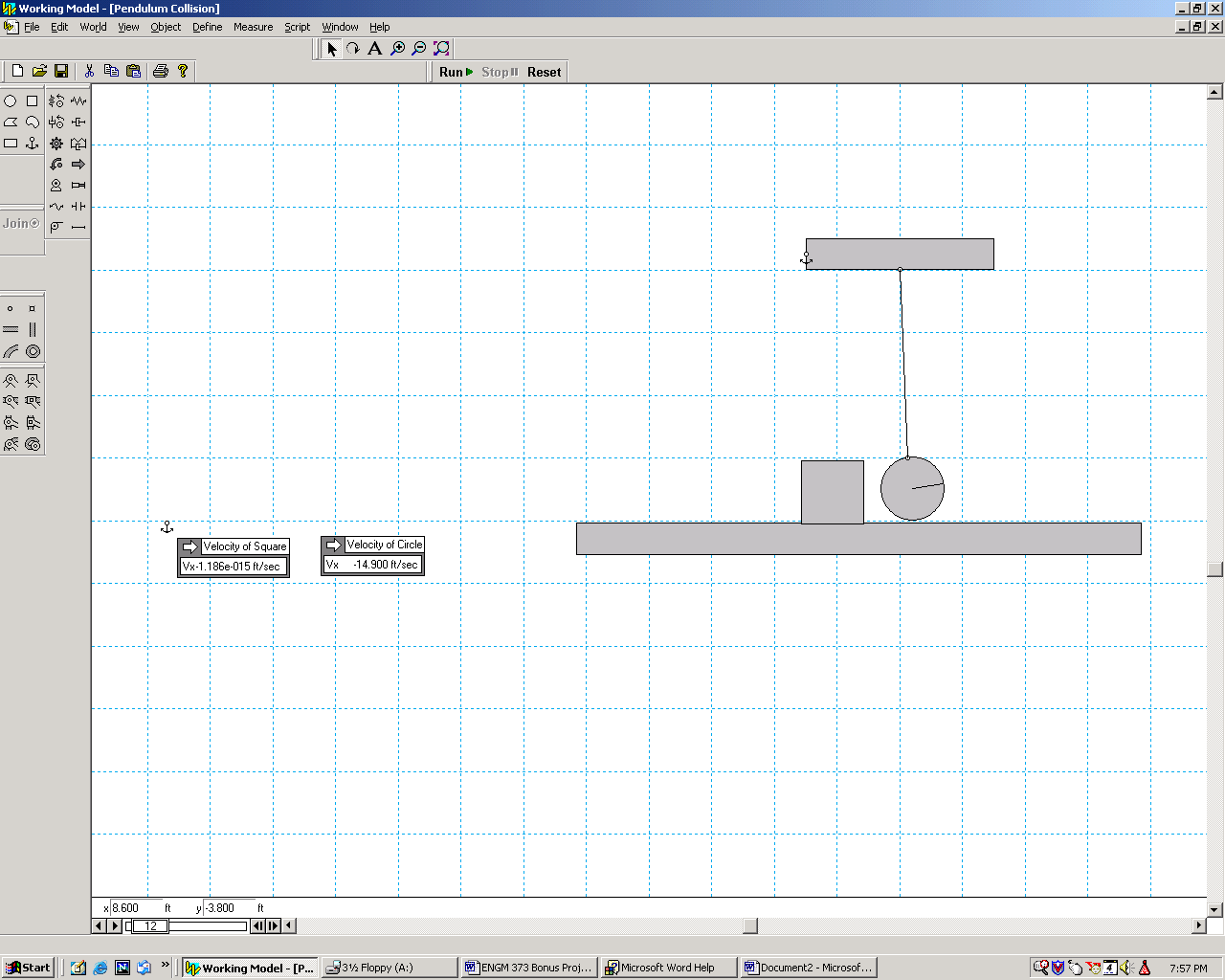
Position of ball and box just prior to impact. Notice velocity
of the ball is 14.9 ft/s, which is higher than that calculated in the previous
part of the problem/
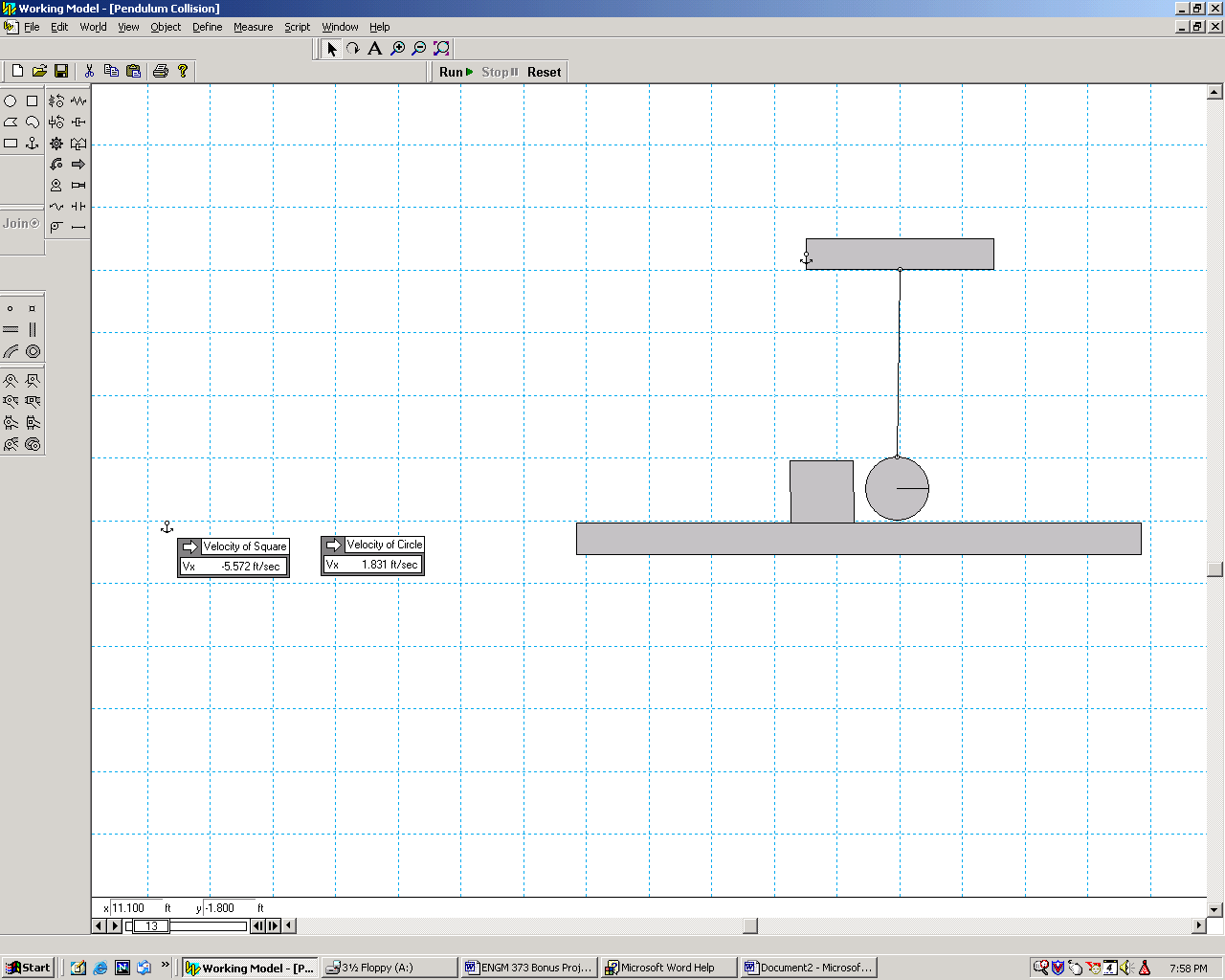
Immediately after impact, the ball travels with velocity 1.8 ft/s and
the box with velocity 5.6 ft/s.
By progressing through the model frame by frame, the velocity after impact of box B is –5.572 ft/s and the velocity after impact of ball A is 1.831 ft/s. These answers are slightly different from those calculated in the previous step. Possible explanations for these differences may be due to additional assumptions made by the Working Model software that are not accounted for in the dynamics calculations. Similarly, assumptions made in the dynamics calculations may not be made by Working Model.
Billiards Modeling
After using Working Model to determine that calculations for a collision problem are modeled in an acceptable manner, Working Model can be used to model other collisions. I chose to model billiard balls because I have been learning how to play this semester.
To view my simulation in Working Model, click here.
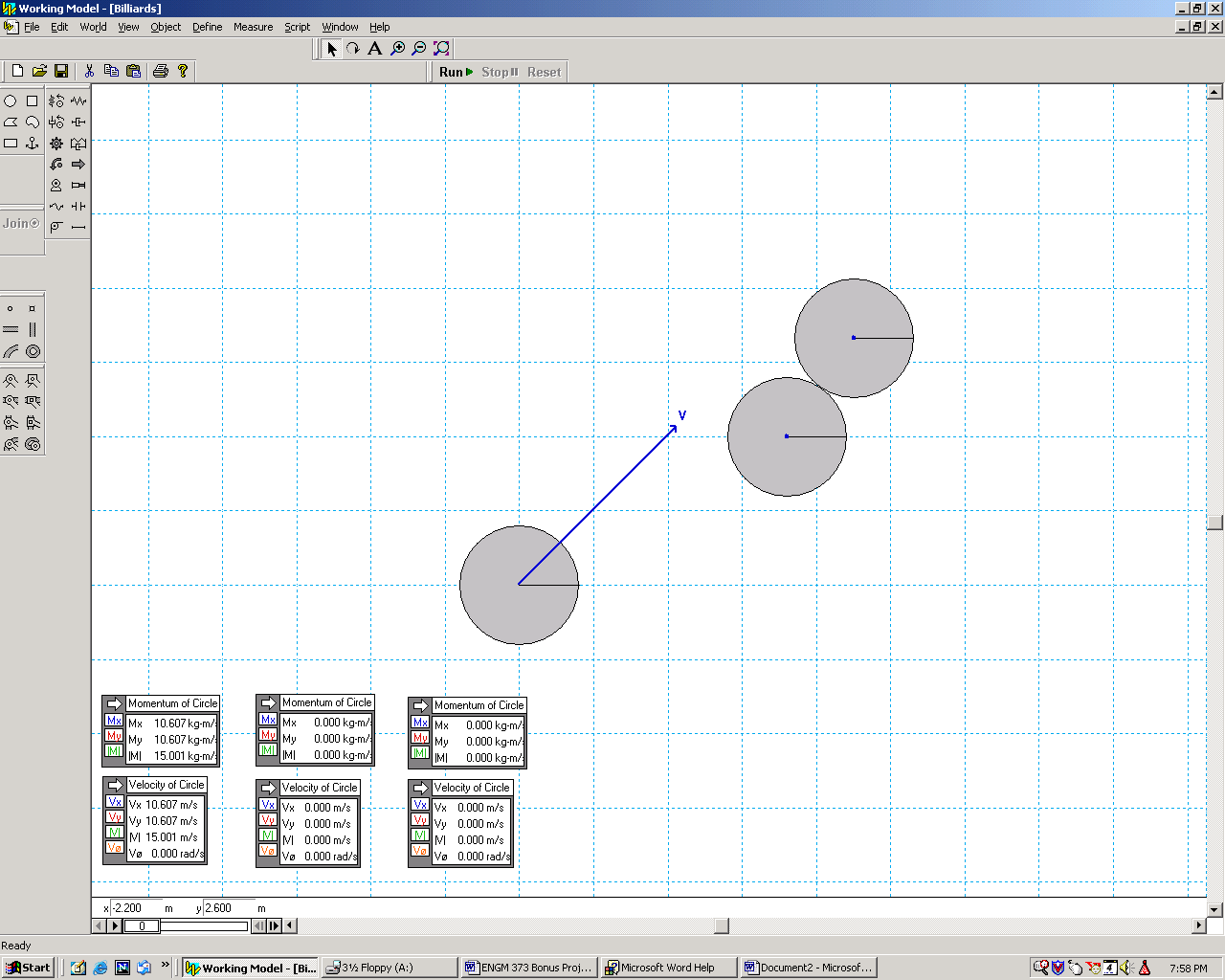
Three billiard balls sit on a pool table.
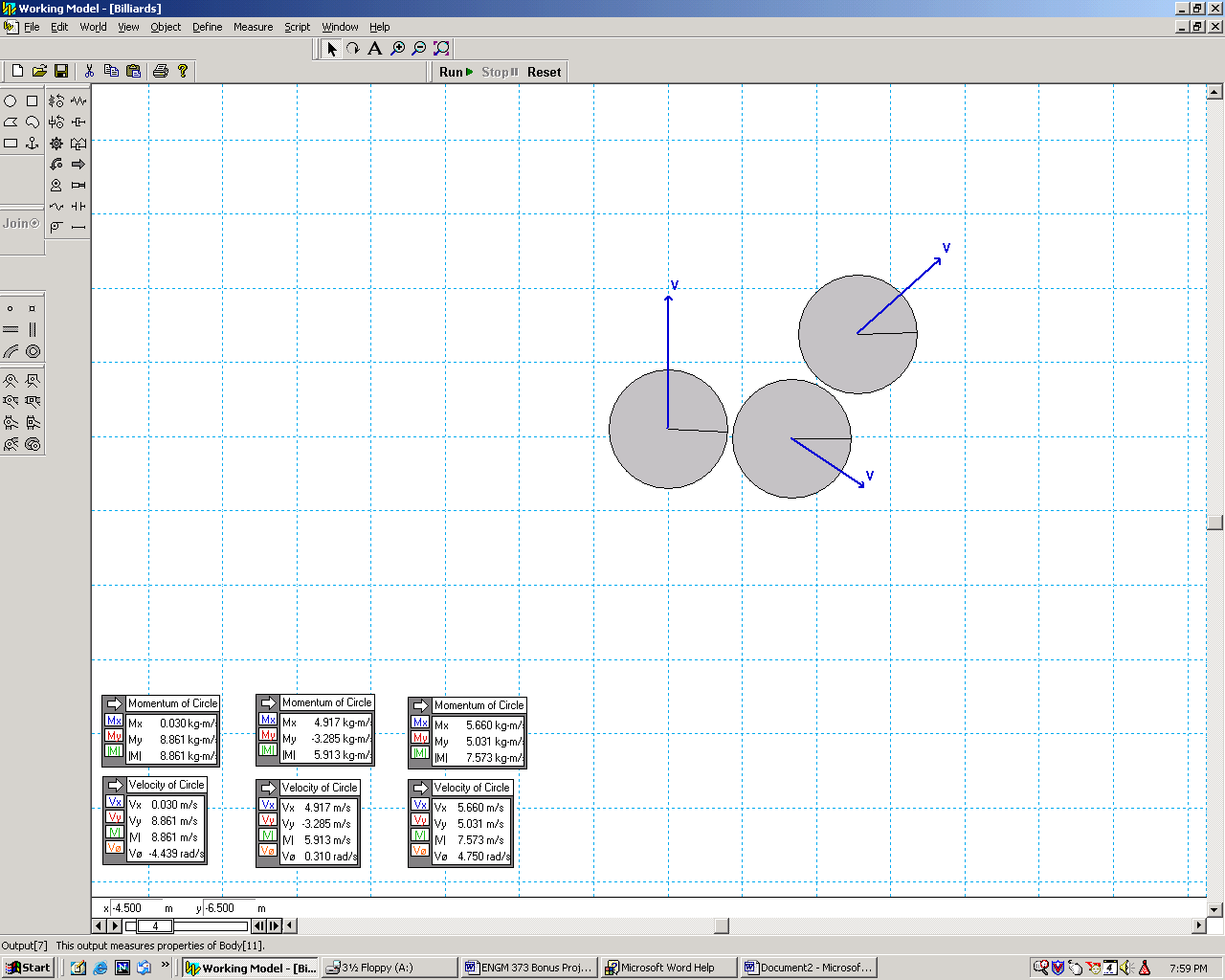
Upon impact, the balls move in different directions.

After the impact occurs, the balls continue to move in different directions.
The center of mass of the system moves in the same direction, however is
not shown on this figure.
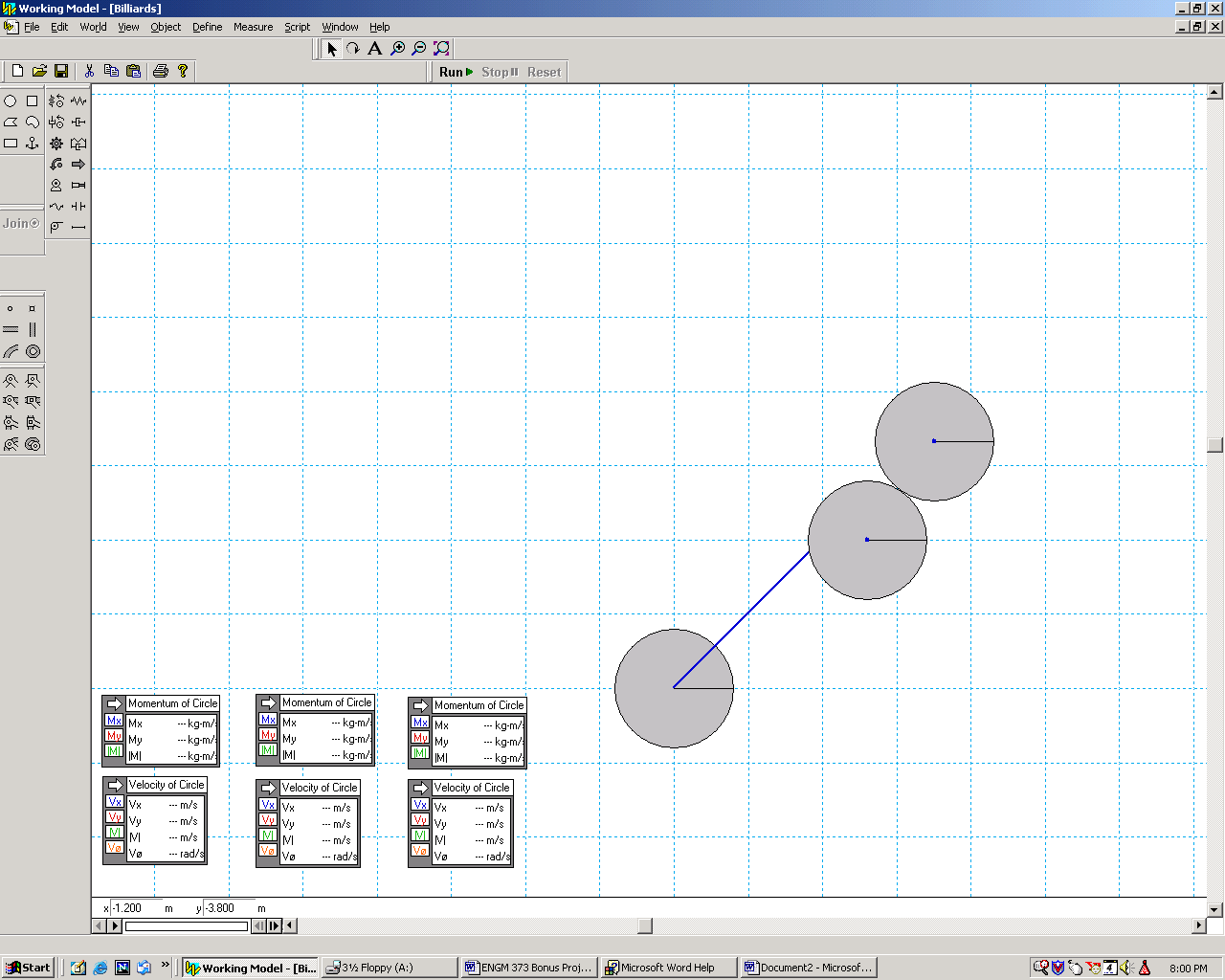
Change the location of the first ball to see how the new angle affects
the collision.
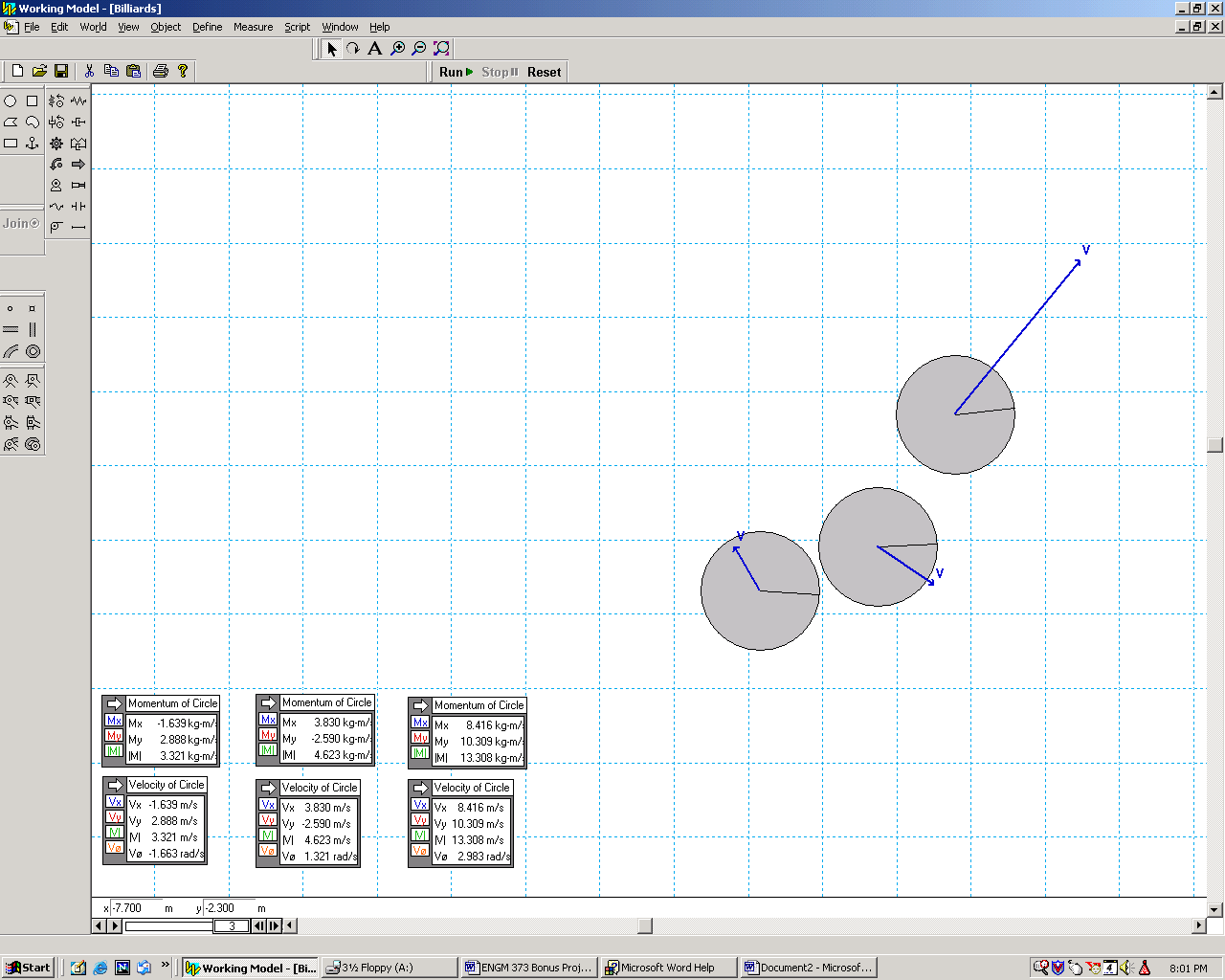
Upon impact, the balls move in different directions, and are also moving
differently than they did in the prior example.
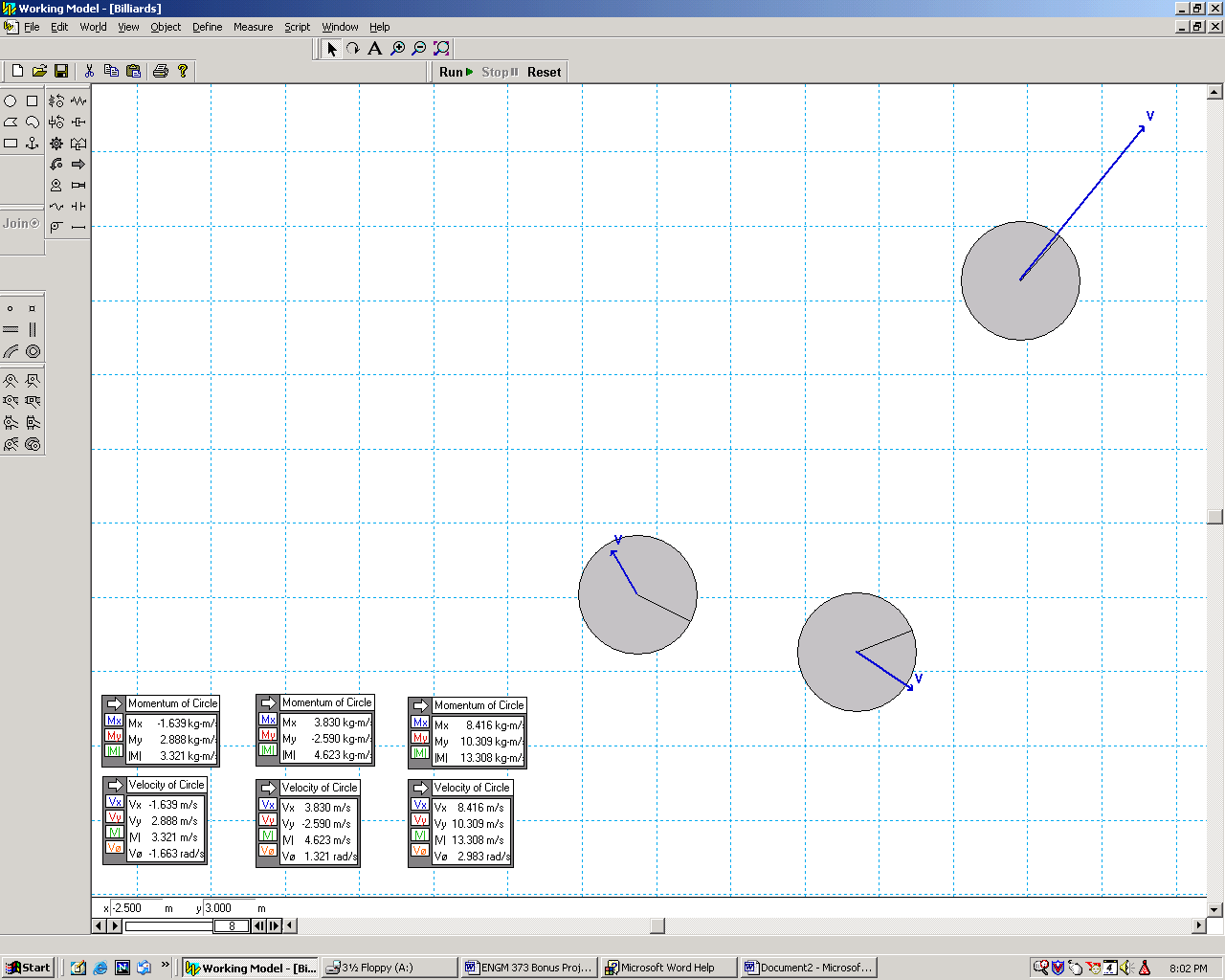
This shows the progress of the billiard balls after impact.