Now at UNL many students are experiencing the thrill of climbing a forty foot wall of rock with only the small handholds an armlengths apart. One false move could mean plummeting to the floor. This distaster is only averted with the use of a safety cable. The friction generated by the cord around the pipe is strong enough to suspend a very heavy person with only a small amount of restrainting force. The ramifications of this friction will be explored in this project.

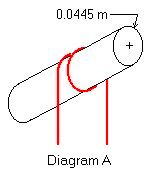
The climbing wall's setup is fairly simple. Two people wear harnesses around their hips. The safety cable is run over and looped once around a metal pipe (Diagram A) forty feet above the ground, and one end is attached to the climber's harness.

The anchor person, or belayer (Diagram B), secures the safety cable by running it through his belaying device. He is then able to keep the rope fairly taut as the other person scales the wall. However, things become interesting when the climber nears the top of the wall because the handholds become smaller and are spaced farther apart. The climber's arms get tired and before they realize it, they slip. Fortunately, the safety cable stops their fall and suspends them in mid-air. If the pipe were frictionless the anchor person wou ld have to support the entire weight of the climber. However, the belt friction between rope and the pipe lessens the amount of force needed by the belayer. The equation that models belt friction turns out to be an exponential equation. It is derived by the following procedure.

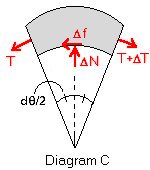
Diagram C is a free-body diagram of the rope over the pipe with the shaded area representing the rope. In this example, T+ delta T (climber) is greater than T (belayer). The normal force is represented by delta N, and the frictional force is represented by delta f. We use mu of static friction because motion still is impending. The free-body diagram is taken over a differential angle theta. The derivation is as follows:

Summing forces in the horizontal direction:

(T+dT)cos(d theta/2) - mu(dN) - Tcos(d theta/2) = 0

Now cos(d theta/2) reduces to 1:

(T+dT)(1) - mu(dN) - T(1) = 0

This reduces further:

dT = mu(dN)

Summing forces in the vertical direction:

dN - Tsin(d theta/2) - (T+dT)sin(d theta/2) = 0

Now sin(d theta/2) reduces to (d theta/2):

dN - (d theta/2)[T+T+dT] = 0

The term (dT*d theta/2) is so small that it is negligible:

dN = T(d theta)

Setting these two equations equal:

dN = dT/mu = T(d theta)

After rearranging, integrate the equation, where T₁ is the tension
in the belayer's cord and T₂ is the tension in the climber's cord:

integral(dT/T)evaluated from T₁ to T₂ = integral(mu*d theta)evaluated from 0 to beta

This gives the following:

ln(T₂/T₁) = mu*beta

Now by expontentiating we have the final equation:

T₂/T₁ = e^mu(beta)

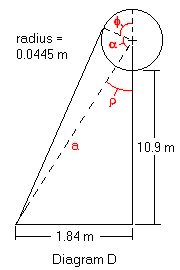
The above equations relates the belayer's rope tension (T₁), the climber's rope tension (T₂), the coefficient of static friction (mu), and the angle that the rope wraps around the pipe (beta). With the above equation and few dimentions from the climbing wall, we can determine force it needed to suspend a person. We were able to measure the radius of the pipe, the heighth of the pipe from a point level with the belayer's hips, and the distance from directly under the pipe to the anchor person as shown in Diagram D. The following procedure was used to find the angle though which the cord contacts the pipe.

To find "a," we use Pythagorean theorem.

a = [(1.84)² + (10.9 + 0.0445)²]^0.5 = 11.1

Knowing the radius, the rise, the run, and a, we can determine alpha and rho.

alpha = arccos(0.0445/11.1) = 89.8

rho = arctan(1.84/10.9 + 0.0445) = 9.54

To find phi, we subtract alpha and rho from 180.

phi = 180 - 89.8 - 9.54 = 80.7

Converting degrees to radians,

X = pi(80.7)/180 = 1.41

To find beta for the original equation,

beta = pi(5)/4 + 1.41 = 5.33

Now that we have beta, we can find the tension in the cord held by the belayer. From the Handbook of Engineering Fundamentals, the coefficient of static friction between a cotton rope on smooth steel is 0.20. My assistant J.R. Andrews was the climber for this project and weighs 711 N. Now we can find the tension that my assistant Brian Dietz must exert are as follows:

T₁ = [(711 N)/e^(.2)(5.33)] = 244 N

This shows that Brian must exert 244 N of force on the rope. The ratio of belayer force to climber force is 0.343. This ratio also decreases rapidly as beta increases because the function is exponential. For example if the rope were wrap once more around the pipe, beta would equal 8.48 and T₁ would equal 131 N. This new ration would be 0.184, which is almost half of the previous ratio.

As the above example shows, wrapping a cord around a pipe is a very effective way to generate friction. Depending on the number of times that the safety cord is wrapped around the pipe, the belayer must pull with only a small fraction of the climber's weight to keep him suspended. Belt friction plays an integral role in the safety of the climbing wall. Not only does friction allow advanced climbers to scale the wall, it is so easily manipulated that the average student can take advantage of this exciting pasttime.

Pictures - Credits