
by Marina Gandelsman
Strain energy is one of fundamental concepts in mechanics and its principles are widely used in practical applications to determine the response of a structure to loads.
Consider a prismatic bar of length L subjected to a tensile force P. The load is applied slowly, so there are no effects due to motion. Such loads are called static loads. As the load reaches its full value P, the bar gradually elongates to L + d.

During this process, the load P gradually moves over the length d and does a certain amount of work. From physics we recall that
W = F * d
However, in this case, the force varies in magnitude (from F=0 to F=P). To find the value
of work done under these conditions, we look at a load-displacement diagram to determine
the manner in which the force varies.
The work done by the load is equal to the area under the curve. As the load is applied, strains are produced and their presence increases the energy of our bar. This strain energy is the energy absorbed by the bar as a result of its deformation under load. From the principle of conservation of energy we know that this energy is equal to the work done by the load, assuming no other energy transfer (such as heat) occurred.
U = W = SL P(x) dx
Sometimes this energy is referred to as internal work, to distinguish it from work done
by the load. The unit of strain energy is the same as work - J (SI) and ft-lb (British).
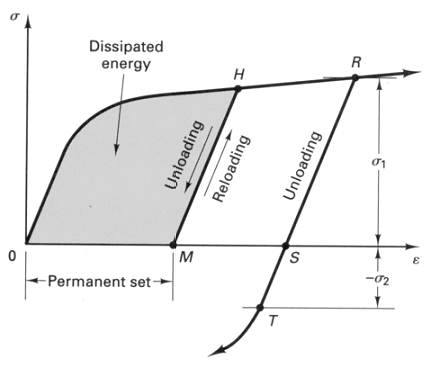
If the force P is gradually removed, the bar will shorten and at least a portion of the
strain energy will be recovered in the form of work. If the material has not exceeded its
elastic limit, the bar will return to its original length L, otherwise a permanent set
will remain.
If the material of the bar follows Hooke's Law, the load-displacement curve is a straight line, P = kd, and the strain energy stored in the bar is:
U = W = kd2/2 = Pd/2
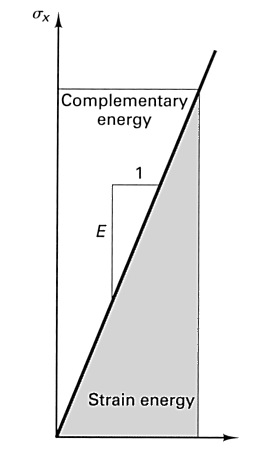
The complimentary energy in the preceding picture is used with Castigliano's theorems
which apply to linearly elastic systems for small deformations as well as Complementary
Strain Energy theorems.
The total strain energy in a bar composed of several sections is equal to the sum of strain energies in each section; however, it is important to realize that the total strain energy for a bar with several loads is not equal to the sum of strain energies for each load.
The total strain energy determined from a load-deformation curve is not really indicative of material since the results will depend on the size of the test specimen. In order to eliminate size as a factor, we consider the strain energy per unit volume (also known as strain energy density). Since P = sA and d = eL, (2) can be rewritten as follows:
U = (se/2)*AL
u = U/AL
u = se/2 = s2/2E
= Ee2/2 (3)
The unit of strain energy density are J/m3 (SI) and in-lb/in3 (British). 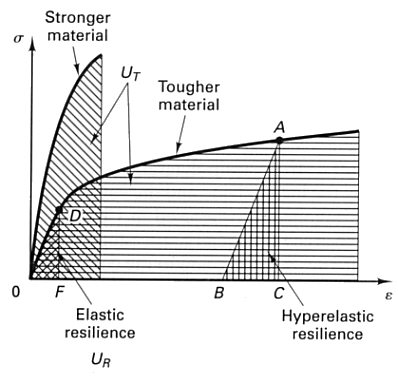
The area under a complete stress-strain diagram gives a measure of a material's ability to absorb energy up to fracture and is called toughness. The larger the area under the diagram, the tougher the material. A high modulus of toughness is important when a material is subject to impact loads. In the inelastic range, only a small part of the energy absorbed by the material is recoverable. Most of the energy is dissipated in the form of heat. The energy that may be recovered when a specimen has been stressed to point A is represented by triangle ABC. AB is parallel to OD since all materials essentially behave elastically upon the release of stress. The area OABO represents the inelastic strain energy (dissipated). The strain-energy density of the material when it is stressed to the proportional limit (D on the diagram) is called modulus of resilience. It is found by substituting the proportional limit spl into one of elastic energy equations:
ur = s2pl/2E
Resilience represents the ability of the material to absorb and release energy within the
elastic range.
Consider a prismatic bar AB in pure torsion under the action of torque T.
When the load is applied statically, the bar twists and the free end rotates through an
angle f. Again, assume the material is linearly elastic and follows Hooke's Law. The
relationship between T and f will also be linear.
From this, we determine that
U = W = Tf/2
Using the equation f = TL/GIp, we can
express strain energy as
U = SL T(x)2/2GIp
dx = T2L/2GIp = GIpf2/2L
If the bar is subjected to non-uniform torsion, the total strain energy is equal to the
sum of strain energies of each segment with constant torque, but again, the total strain
energy of a structure supporting several loads is not equal to the sum of strain energies
from each load.
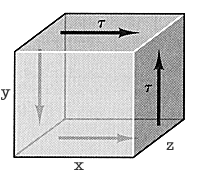
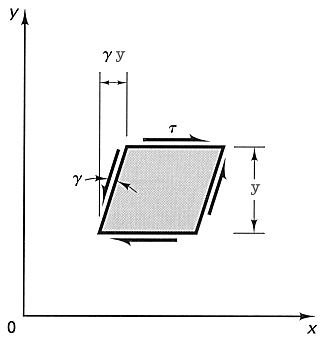
Consider an element of dimensions x, y, and z subjected to shear load t. As this element is deformed, the force on top plane reaches a final value of txz. The total displacement of this force for a small deformation of the element is gy. Therefore,
W = U = 1/2 t xz * gy = 1/2 tg V = 1/2 t2V/G
The strain-energy density in this case is
u = 1/2 tg = 1/2 t2/G
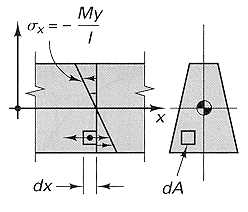
Consider a beam in pure bending by couples of moment M. Its material follows Hooke's Law
and rotations are small. The normal stress varies linearly from the neutral axis and s = -My/I. >From U = s²/2E and the
stress equation, we get
U = M2L/2EI
Substituting q = ML/EI, we get
U = EIq2/2L
If the bending moment in a beam varies along its length, we can obtain the total strain
energy by applying one of the preceding equations to an element of the beam and
integrating along its length. From dq = 1/r
dx = d2v/dx2 dx, we get
U = SL M(x)2/2EI
dx = SL EI/2 (d2v/dx2)2
dx
The previous equations only consider the effect on bending on the beam. If shear forces
are also present, additional strain energy will be stored in the beam, however, this
energy is negligible in beams where L >> t. If a beam supports a single load (either
point load P or moment M0, we can determine either deflection d (for P) or angle of rotation q (for M0)
from strain energy. The deflection is measured along the line of action of the load and is
positive in the direction of the load. The angle of rotation is the angle of rotation of
the beam axis at the point where the moment is applied. We can obtain the following
equations:
U = W = Pd/2
U = W = M0q/2
This method is limited in its applications because only one deflection (or angle) can be
found and that deflection (or angle) must correspond to the load (or couple).
The equations demonstrated here are fairly basic and simplified in several ways. Only the
perfectly elastic bodies do not dissipate any energy and thus can store all of the work as
recoverable energy. Most real-life materials are not elastic. A lot of research is
concerned with what happens in the postelastic regions, however, this discussion is beyond
the scope of this paper.
Mechanics of Materials
, Gere & Timoshenko, 4th edition, PWS Publishing© 1999 by Marina Gandelsman. Distribute freely (I borrowed quite liberally from my sources, obviously :)