The machines are huge, measuring 213 feet to the top of the tower and a whopping 290 feet to the top of the blades.  With a machine this big, ignoring the statics of the system could be devastating and ultimately result in malfunction or, in a worst-case scenario, the machine's collapse and a huge safety risk.

The machine is composed of three main components:  the tower, the blades, and the nacelle(pictured below)--which sits atop the tower and includes the gear box, low- and high-speed shafts, generator, controller, and brake.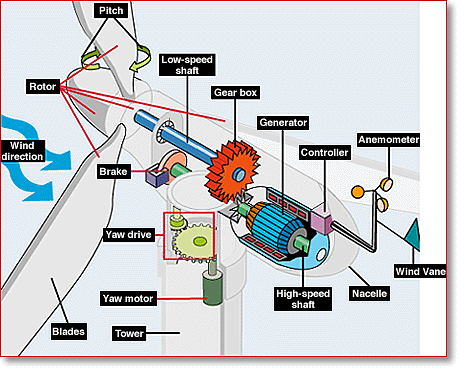 

When the wind blows past the blades, a moment about the central hub is produced.  This is where the power generated by the windmill is developed.  There are numerous other forces, however, and these other forces either directly counteract the moment about the central hub, or they produce a force directed along the axis of the central hub.  The distribution of the forces is actually too advanced to be derived using concepts learned in a statics course, but can be described using some principles of aerodynamics.  A description of some of these aerodynamic principles is available at the link below:
http://metp02.mw.tu-dresden.de/Merz_McLellan/windenergy/Aero.htm
These principles give us formulas which can be used to determine some forces acting on the turbine even if we don't understand how they are derived.

Let us start with a safety question:  "Will the tower fall over?".  As you can see, this is an important question, and I would like to think that somebody investigated the situation before the tower was built.  Let us double check, in case the engineer working on the project was delinquent:

The force exerted on the hub is obtained from the equation for thrust(obtained from the web site listed above--not derived).

                Thrust (N) = [(Vup_wind + Vdown_wind)/2]* Dair*Aswept*(Vup_wind - Vdown_wind)...Equation (a):
                Where:
                Dair = approx. density of air = 1.29kg./cu.meter
                Aswept = area of the turning blades = radius^2*pi

For our turbines, the radius of the circle formed by the turning blades equals:

                radius = 77 ft = 23.47 m
                Aswept = 1730.46 m^2
The maximum thrust for a horizontal axis turbine is when Vdown_wind = Vup_wind/3 (condition for maximum power), and equation (a) then becomes:

                Maximum Thrust = Dair*Aswept*(Vup_wind^2)*(4/9)

Wind turbines are controlled to shut down in storm conditions and the overturning moment is principally determined by the maximum output power of the wind turbine. However, providing the output power of the wind turbine can be controlled, the thrust developed is equivalent to maximum power output. The overturning moment can then be obtained by multiplying by the height of the hub above ground level.

For our turbines, maximum output occurs when the wind speed is:
                32.8 miles/hour = 14.66 m/s
                Thrust = 1.29*1730.46*(14.66^2)*(4/9) = 213.224 kN
                Height of tower = 213 ft = 64.92m
                Moment about base = 213.224kN*64.92m= 13,843kN*m

 Now we must determine the moment about the base that the base is able to withstand.  To do this, we must use some information obtained from the Lincoln Electrical Systems webpage at  LES: Renewable Power: Construction Photos   and    LES: Renewable Power: Questions and Answers.  We find that:
                Circular base = 14 feet diameter = 7 feet radius = 4.2672 m radius
                There are 120 anchor bolts that are:
                31 feet long = 9.4488 m
                200 pounds = 90.718 kg
 

Using data obtained from  MatWeb.com, we find that:
                        Bolt density = 7.87 g/cc = .01735 lb/cc = 491.297 lb/ft^3 = .00787 kg/cc
                Volume of each bolt = 90.718 kg/(.00787 kg/cc) = 11,527.1 cc
                Cross-sectional area of each bolt = 11,527.1cc/944.88cm = 12.2 cm^2
                Tensile strength of each bolt = (56,500 N/cm^2)*(12.2 cm^2) = 689.271 kN
 

We know that there are 120 bolts around the perimeter, but they each contribute a different moment since they are located at different distances from one side of the base.  The sum of the moments can be calculated as:
, which is a summation of the contribution to the total moment provided by each bolt.  Since each bolt is located a distance of only:
               Arc distance = (4.2672 m)*2*(pi)/120 = .2234301m
                Straight-line distance = .2234045m
from each other, it is reasonable to assume that they make up a continuous force which can then be used in an integration.  The integration is based on this assumption and on the following diagram:

The integral is thus:

which evaluates to:

which equals:
                 Moment about base that tower can withstand = 352,951 kN*m

As you can see, the design of the tower anchoring system allows for a safety margin of:
                Safety margin % = (Calculated moment/Maximum withstandable moment)*100 = (352,951/13,843)*100 = 2,549%
This is a very acceptable safety margin.

 There is one more thing which we can do using our knowledge of statics, and that is to calculate the maximum lead of the bolt that will still be self locking.  Using data from  http://www.physlink.com/ae139.cfm,we find that the coefficient of static friction of steel on steel is:
             Coefficient of static friction of steel on steel = .74
and the maximum lead is calculated as:
              radius of bolt = (12.2cm^2/pi)^(1/2) = 1.97 cm

As you can see, this is a rather large lead, although this lead would be significantly reduced if there was any lubrication applied(as there frequently is).  However, the safety margin is still adequate, and we can safely conclude that the design of the wind turbine is sound.