Stresses in Beams
Prepared by Wei-Siong Tan
For EM325: Mechanics of Elastic bodies

I have always enjoyed watching Martial Arts performances. One of the things that I enjoy most is to watch the performer as he chops (breaks) a wooden board into two with his bare hands. However, you might have realized that most of the time the performer would only chop on the surface of the wooden board rather than on the side of the wooden board.
The reason for this is rather simple. The performer would need to apply much greater load on the side in order to break the wood compared to the surface of the wooden board. This can be proved analyzing the two cases.
Case 1 and Case 2 have all the same properties (material, width, length and height) except for their orientation. In Case 1 the load is applied on the surface of the wooden board and in Case 2 the load is applied on the side of the wooden board.
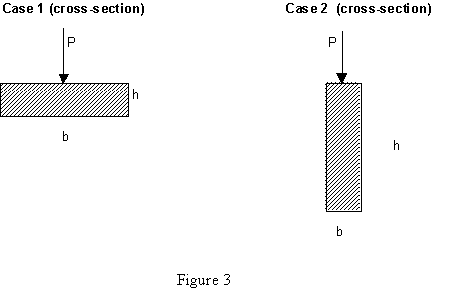
Analysis
Basically our analysis can be divided into two sections: Statics and Mechanics of Material. Our main goal is to determine the load P to break the board in bending (PN) and in shear (PS). Comparing PN and PS, we can determine the minimum load that is required to break the board into two parts. This analysis is done for both Case 1 and Case 2.
We also further our analysis by looking at how the height (h), base (b) and length (L) changes PN and PS. In the final part of our analysis we will look at a special case that examines the relationship between the load P with the shape of the board.
Statics
We begin our analysis with statics. We first draw the free-body-diagram. Then using equations of equilibrium we can determine the support reactions in the wooden board.
Equilibrium Equations:
After determining the reactions in the wooden board we then proceed to construct the shear-force and bending-moment diagrams. From the shear-force diagram shown in Figure 5, we see that the shear force at end A of the beam (x = 0) is equal to P/2 (reaction at point A) and remains constant to the point of application of the point load P at the center. At that point, the shear force decreased abruptly by an amount equal to P. In the right-hand part of the wooden board, the shear force is again constant but numerically equal to the reaction at B.
The bending moment in the left-hand part of the beam increases linearly from zero at the support to PL/2 at the center. In the right hand part, the bending moment decreases linearly to zero (x = L), as is shown on Figure 5.
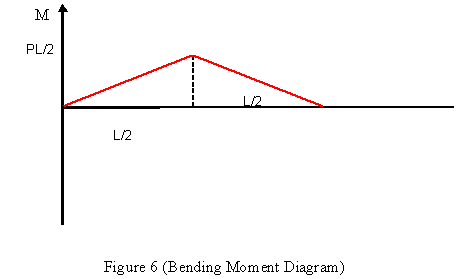
From the shear-force and bending-moment diagram we can find V (max) and M (max).
V (max) = P/2
M (max) = PL/4
Mechanics of Material
We will now use Mechanics of Material for the next part of our analysis. We will first determine the allowable normal stress and allowable shear stress.
Allowable Normal Stress
Allowable Shear Force
Sub (3) into (2)
The maximum value of the shear stress occurs at the neutral axis (y =0), where the first moment Q has its maximum value.
Since,
Therefore
From equation 1 and equation 4
We can now look at Case 1 and Case 2. Equation 5 and equation 6 will be applied for both Case 1 and Case 2. The properties of the wooden beam are given as follow.
Case 1
Case 2
Conclusion 1
The minimum load required to break the wooden board into two parts for Case 1 is PN = 856 N, and is due to bending. For Case 2 a minimum load of PS =3360 N is required, and is due to shear. From this we conclude that the minimum load to break the wooden board into two is higher if the wooden board is oriented as Case 2.
The shear stress for both Case1 and Case 2 are found to be the same. This implies that the orientation of the wooden board has no effect on the shear stress. This can also be seen from equation 6.
Further Analysis:
Parametric StudyWe now look at the relationship between height (h), base (b) and length (L) with PN and PS. This is done by graphing PN vs. h, PN vs. b, PN vs. L, PS vs. h, PS vs. b and PS vs. L. This is again done for both Case 1 and Case 2. Clisk on the link to take you to these plots
Conclusion 2
From the graph PN vs Height, we can conclude that PN has a quadratic relations to height. Which means that as height increase so will PN. As for PS vs Height, we found a linear relationship. This implies that, as height increases so will PS.
Form the graph PN vs Base and PS vs Base; we found the relationships to be linear. Which means that as the base increases so will PS and PN.
As for PN vs. Length, we found the relationship to be inversely proportionate. As the length of the wooden board increases PN will decrease. Finally we found that PS is not effected by the length.
This conclusions holds for both Case1 and Case 2. By analyzing the results that we reached a few conclusions. We conclude that it is easier to break the wooden board for both PS and PN by applying the load on the surface of the wooden board (Case 1) rather than on the side (Case 2). We also found that as height and base of the wooden board increases, it makes it more difficult to break the wooden board. This is again true for both PS and PN. As the length increases we found that it is easier to break the wooden board with bending load (PN). The length has no effect on the shear load that is required to break the wooden board.
Therefore the best way to break a wooden board is to apply the load on the surface of the wooden board (Case1) that has a short height and base, and a long length.
Special Case
Usually in a Karate performance, the performer would break several wooden boards that are stacked. Up to now we have analyzed the minimum required load to break the wooden board with relations to the area the load is applied, the height, the base and the length.
Now we will look at a special case where the wooden boards are stacked. We will look at the relationship between the load P with the shape of the board. The shape of the wooden board that we are referring to can be seen on Figure 9 and Figure 10.
If a wooden board is shaped as Figure 9, it will require a lower load P and thus break more easily. There are basically two reasons for this. The first reason is because of the smaller height in the wooden board. From the graph PN vs. Height and PS vs. Height, we have concluded that a smaller height would break more easily.
The second reason is due to the fact that the surfaces of the boards are not touching. When the load is applied the wooden boards will undergo a small amount of bending. If the surfaces of the wooden board are not touching, there will not be any friction between each wooden board that will make it more difficult to break. This implies that the performer would be breaking the wooden boards one at a time rather than as a block.
Figure 10
Department of Engineering Mechanics Phone: (402) 472-2377 W317.4 Nebraska Hall FAX: (402) 472-8292 University of Nebraska-Lincoln E-mail: dgsem@unl.edu Lincoln, NE 68588-0526 Web: http://www.unl.edu/emhome/em.html