The travel of a puck and collision of balls
Tyler Tolineís Extra Credit Assignment
Hello my name is Tyler Toline and I am a junior at the University of Nebraska majoring in Mechanical Engineering.† At the present moment I am taking a Engineering Mechanics class titled Dynamics.† I have chosen to do an extra credit assignment for this class trying to boost my grade to the next level and here it is.
The extra credit assignment has two parts.
Part A: Take a problem from our textbook:
(Vector Mechanics
for Engineers, Dynamics)
by
Ferdinand P. Beer and
E. Russell Johnston Jr.
†And then work it out by hand using the steps taught during class.† After that I had to use a program titled:
Working Model
Version 5.1.2.53
MSC. Software
To find out if my calculations were correct.
Part B: Use a problem with real world applications and then use working model to see if my calculations are correct.†
So Here we go:
Part A:
Chapter 12 # 5 on page 682
††††††††††† A hockey player hits a puck so that it comes to rest in 9 seconds after sliding 30 m on the ice.† Determine a) the initial velocity of the puck, and b) the coefficient of friction between the puck and the ice.†
Solution:
The first thing that I need to do is set up my free body diagram and my inertia diagram:
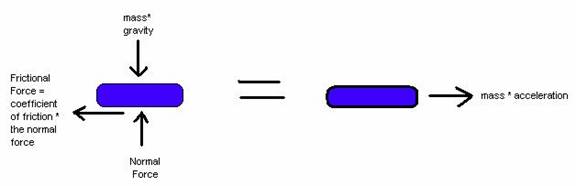
Using this diagram I set up my summation of forces to find out my unknowns
Σ Forces in the y
direction vertical with up being positive = 0 = N Ė mg ► N = mg
From this calculation I have found out that N the normal force is equal to the mass of the puck * the acceleration due to gravity
Σ Forces in the x
direction horizontal with left being positive = ma = - Ff = ma
From this calculation I have found that the mass of the puck times the acceleration of the puck is equal to the negative force of friction, and since the force of friction equals the normal force N times the coefficient of friction μ that gives me
- μ * mg = ma
Since the mass is the same on both sides that can cancel out leaving us with
- μg = a
finally
†μ = -a/g (1)
With that equation we can solve for the coefficient of friction after we find the acceleration.† So now we will use our equations of motion to solve for a and Vo the initial velocity.† We have two motion equations that will be used to solve this problem first:
V2 = Vo
2 + 2aΔx
This
equation says that the final velocity squared equals the initial velocity squared
+ two times the acceleration times the change in position, which is given from
the initial conditions and equals 30 meters.†
Since the initial velocity is zero this formula simplifies to
Vo 2 =
- 2*a*30
Which leads to
- Vo 2/60† = a (2)
That is as far as we can go with that equation.† That brings us to the last equation that we will need to solve this problem.
x=xo + Vo*t
+ (1/2)a*t2
This equation says that x the distance traveled is equal to the initial distance plus the initial velocity times t the time + one half the acceleration times the time t squared.† The time is another one of the initial conditions and it equals 9 seconds we also know that the initial distance so using that information we have
30 = 9Vo + 40.5a
(3)
Using that information and subbing the value for a we found earlier in equation 2 brings us to
9Vo - .675Vo2
Ė 30 = 0
Using the quadratic equation I have found that
Vo = 6.67 m/s
Now I use that value to find out the value for a using subbing the value for Vo back into equation 2 gives me
a = -.74148 m/s2
Finally I sub that value of a back into equation 1 and that gives me a value for
μ = .07558
Now that I have solved the problem by hand for the values in bold I now need to use the Working Model software to see if I am correct.† I decided to throw a little twist into the game and see really how good I am and so what I did is I used the values that I found for Vo and μ to see if I get the original initial conditions back out.† Now is your chance to see if I am correct in my work, click the link and you can see the values for Vo and μ and then press run to see if I am correct.
Pretty close I would have to say. The only differences in the answers are going to have to do with the fact that Working Model will not allow me to put in the exact values only to a few decimal spots.† Having done that I will move on to part B.
Part B:
Now
part B was a bit more difficult for me.†
I had a very hard time figuring out what I wanted to do and what I
wanted to show the world.† I had many
attempts and many failures trying to find something that would be challenging
and yet beneficial to the general public.†
After searching for a long time I decided to just look at the class in
general and think of some topics that I had trouble with and then go from
there.†
After searching for awhile I came up with two topics momentum and the
coefficient of restitution.† Both are
simple but yet very challenging concepts. From now on I will refer to the
coefficient of restitution as e.† After
searching on the internet for topics that include e, I found that it is most
used in the golfing industry where there are many rules for how bouncy a golf
ball can be, and therefore rules on what e can be.† Well what I propose is that I will use one equation for momentum
and one for e and then I will put then together and see if it is true that when
two balls are collided that have equal masses, the e value and the two initial
velocities are the only things that factor into the final velocities.
My first equation is.
mV1 + mV2 =
mVí1 + mVí2
This is my sum of momentums equation.† It says that the sum of the masses times the velocities before the collision will equal the sum of the masses times the velocities after the collision. †Since we will be working with identical masses this simplifies to.
V1 + V2 =
Ví1 + Ví2
Then I will use this equation and solve it for Ví1 which is the velocity of ball 1 after the collision.
Ví1 =V1 + V2 -Ví2 (1)
After doing that I will now turn to my second equation, which is.
Ví2 = Ví1 + e*( V1 - V2)
(2)
This equation is the equation used when you have a collision of two non-elastic bodies. Nothing in this world is totally elastic and also nothing in this world is totally plastic.† Being elastic means that a particle will absorb some of the energy during a collision.† That is where the e value comes into play.† The e value is titled the coefficient of restitution and is also sometimes called the coefficient of elasticity.†
What I will now do is sub equation 1 into equation 2.† The new equation is
Ví2 = V1 + V2 -Ví2 +
e*( V1 - V2)
When simplified
2Ví2 = V1 + V2 + e*( V1
- V2)
and finally
Ví2 = (V1 + V2 + e*( V1
- V2))/2
Now the way that I have proved that the e value really is the major component in collisions is I have set up a collision and worked out the values on paper.† The collision that I have set up looks a little something like this.
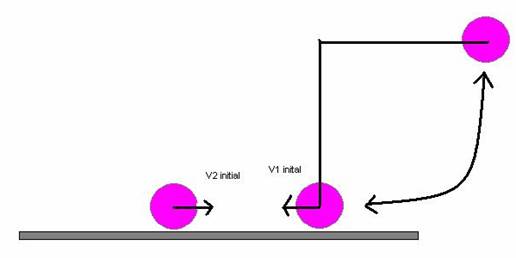
and after the collision it looks like this
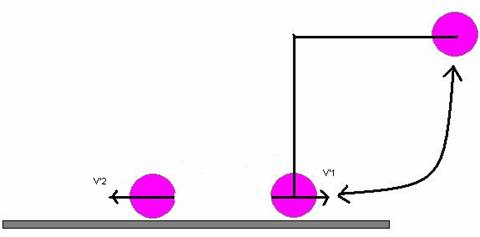
The initial velocity of ball 2 is a value that I randomly chose.
V2 = 4 m/s
The initial velocity of ball one is a bit more difficult to compute.† I will use the sum of energies equation to compute this value. For a pendulum neglecting all friction.
Max Potential Energy = Max kinetic energy
The formula for potential energy
PE = mgh
m being the mass, g being gravity, and h being the height above the impact level, or length of the cable for practical purposes.
And the formula for kinetic energy is
KE = (1/2)mV2
m still being the mass times one half the velocity squared.† Setting the two equations equal to each other and simplifying I come up with.
V = √( 2gh)
So that brings me to the problem.† I have set my height as 3.4 meters being the length of the string and that will give me an initial velocity of
V1 = -8.1 m/s
The velocity is negative because the ball is traveling in the negative x direction.†
After doing all this I calculated the theoretical values of Ví2 for various e values neglecting air resistance and friction because this is a perfect world isnít it.† I have also set up many models on the Working Model software to test my values, to see the simulations just click on the link and then press the run button.† My values are as follows:
|
e value |
Theoretical velocity (m/s) |
Working model Simulation |
|
0 |
-2.05 |
|
|
.15 |
-2.9575 |
|
|
.3 |
-3.865 |
|
|
.45 |
-4.77 |
|
|
.6 |
-5.68 |
|
|
.75 |
-6.58 |
|
|
.9 |
-7.49 |
|
|
1 |
-8.1 |
I hope that after looking through the models you along with I will have come to realize that the coefficient of restitution is a pretty neat idea and it really does play an important role in all collisions which may also help me later in my life since I am also a member of the football team.† I figure as long as I have a low e value no one will be able to get away from me.†
In conclusion this project was really pretty entertaining working with the Working Model and I hope that you learned a lot from my research and hard work.