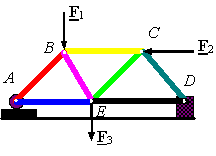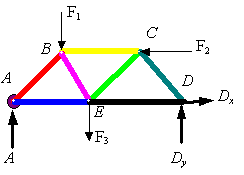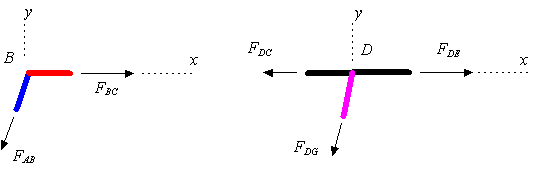The
analysis of trusses
A truss: A truss is a structure
made of two force members all pin connected to each other.
|
|
The method of
joints:
This method uses the free-body-diagram of joints in the structure to determine
the forces in each member. For example,
in the above structure we have 5 joints each having a free body diagram as
follows
|
|
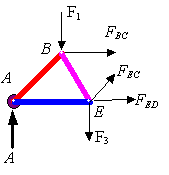
Note
how 
on the joints A and on the joint B. For each joint one can write two
equations (
). The moment equation is trivially satisfied since all
forces on a joint pass trough the joint. For example, for the above truss we
have 5 joints, therefore we can write 10 equations of equilibrium (two for each
joint). In the above example there are seven unknown member forces (FAB, FBC, FCD,
FED, FEC, FBE, FAE) plus three unknown support reactions (A, Dx, Dy), giving
a total of 10 unknowns to solve for using the 10 equations obtained from
equilibrium.
|
|
The method of
sections:
This method uses free-body-diagrams of sections of the truss to obtain unknown
forces. For example, if one needs only to find the force in BC, it is possible
to do this by only writing two equations. First, draw the free body diagram of
the full truss and solve for the reaction at A by taking moments about D.
Next draw the free body diagram of the section shown and take moments about E to find the force in BC.
|
|
In
the method of sections one can write three equations for each free-body-diagram
(two components of force and one moment equation).
Things to
consider:
·
Zero force
members:
Some members in a truss cannot carry load. These members are called zero force
members. Examples of zero force members are the colored members (AB, BC, and DG) in the following truss.
|
|
Consider
the following free-body-diagrams
|
|
If
you sum the forces in the y-direction
in the left free-body-diagram, you will see that FAB must be zero since it is not balanced by another
force. Then if you sum forces in the y-direction
you will find that FBC
must also be zero. If you sum the forces in the y direction in the right free-body-diagram, you will see that FDG must be zero since it is
not balanced by another force.
·
A redundant
joint:
Sometimes a joint is redundant. For example, in the following free-body-diagram
the load is directly transmitted from each member to the one opposite it without
any interaction.
|
|
By summing forces along the y-direction one will get F2=F4,
and by summing forces along the Y‑direction
one will get F1=F3.
·
Redundant
members: Sometimes
a structure contains one or more redundant members. These members must be
removed from the truss, otherwise one will have an insufficient number of
equations to solve for the unknown
member forces. Slender members are not very useful in compression since they
buckle and, as a result, lose their load carrying capability. For example, in
the following truss one of the two members AC
or BD is redundant. To solve the
problem, we remove member BD which
will go into compression as a result of the applied loading (i.e., the diagonal
AC will have to increase in length
and the diagonal BD will have to
decease in length for the structure to bend to the right). If we did not remove
this member we would have 9 unknowns (five member loads and four support
reactions) and only 8 equations (two for each joint).
|
|
·
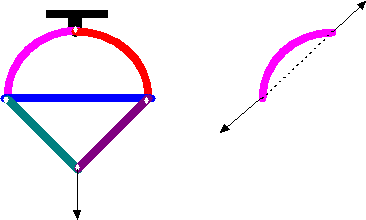
Mechanisms: Sometimes there is too
much freedom in a structure. For example, the following structure cannot carry
any load since it will collapse under the load.
|
|
|
|
·
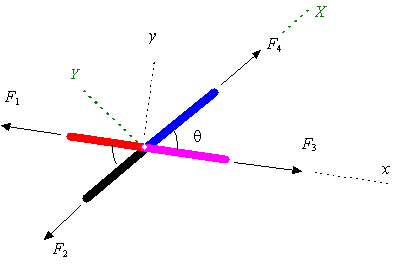
Curved members: Remember that the two
forces acting on a two-force-member are along the line connecting the two
points on which the loads are applied.
ã Mehrdad Negahban and the University of Nebraska, 1996-2006.
All rights reserved
Copy and distribute freely for personal use only
Department of Engineering Mechanics,