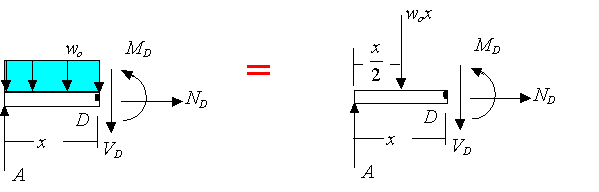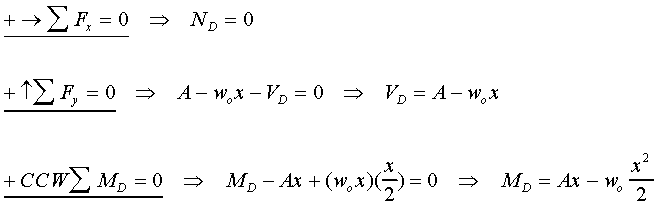Internal forces
As one can calculate the forces and moments transmitted through joints between members, one can also calculate the internal forces which one part of a member exerts on another. To calculate these internal forces, simply draw a free-body diagram of only part of the member, cutting through the member at the point you are interested in knowing the forces and moments. For example, consider the following member
If you are interested in knowing the forces and moments that are transmitted through the member at point D, you can draw the free-body-diagram of the portion to the left of D to get
For the body to be in equilibrium one must have
In this example, is the axial force exerted by the right side of the bar on the
left side of the bar at D,
is the shear load exerted by the right side of
the bar on the left side of the bar at D,
is the bending moment exerted
by the right side of the bar on the left side of the bar at D.
The example shows the basic elements of how one find the internal forces at a given point in a member. Like any other constraint, one must introduce a force or a moment for every way in which the motion of one side of the point is restricted by the other side. For example, in the above the right side of D exerted restricts the left side from freely moving along the axial direction, transverse to the axial direction, and restricts its free rotation. Consequently, two forces and one moment are introduced to enforce the restriction.
Note: the forces and moment applied by the left-hand side onto the right-hand side are equal in magnitude but opposite in direction to the forces applied by the right-hand side on the left-hand side.