Wedges and screws

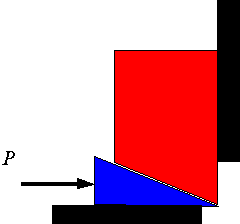
Wedge: A wedge is in general a triangular object which is placed between two objects to either hold them in place or is used to move one relative to the other. For example, the following shows a wedge under a block that is supported by the wall.

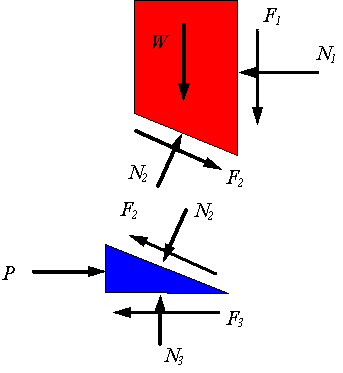
If the force P is large enough to push the wedge forward, then the block will rise and the following is an appropriate free-body diagram. Note that for the wedge to move one needs to have slip on all three surfaces. The direction of the friction force on each surface will oppose the slipping.

Since before the wedge can move each surface must overcome the resistance to slipping, one can assume that

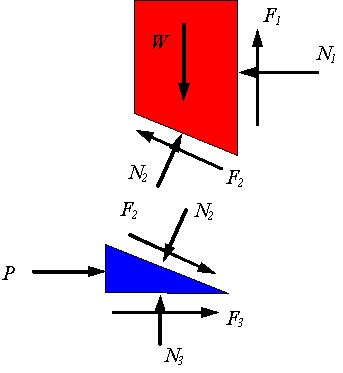
These equations and the equations of equilibrium are combined to solve the problem. If the force P is not large enough to hold the top block from coming down, then the wedge will be pushed to the left and the appropriate free-body diagram is the following. Note that the only change is the direction of the frictional forces. A similar analysis to the above yield the solution to the problem.

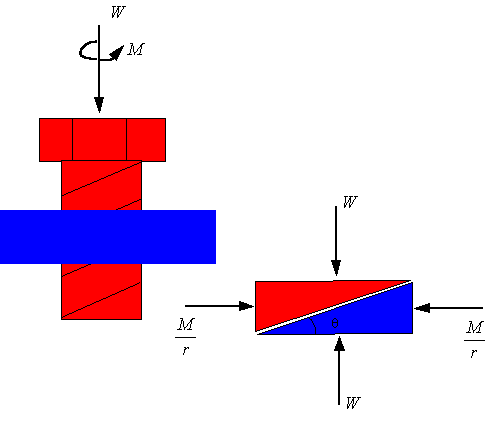
Screws: One can consider a screw and a bolt as a combination of two wedges. One wedge is obtained from opening the helical treads of the screw and the other will come from opening the helical threads of the bolt. For example, if one opens one revolution of the thread of a screw having a lead of l and mean thread diameter 2r, one gets the following wedge where is the lead angle.

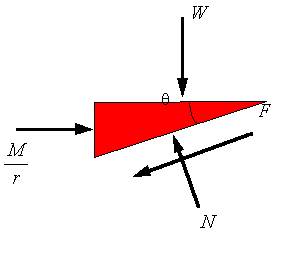
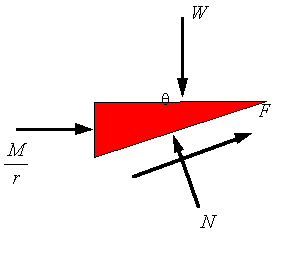
Now consider the situation where a screw is in a bolt or threaded hole. In the picture the screw is being pushed into the hole as the screwing moment is trying to unscrew it. Depending on the lead angle, the magnitude of the axial load W, and the magnitude of the applied moment M, either the axial load will dominate and the screw will move down or the moment will dominate and the screw will move up.

If the axial moment is sufficient to unscrew the screw, then the frictional force will oppose moving up of the screw threads and one will use the following free-body diagram for the wedge.

If the axial load is large enough to screw the screw into the bolt, then the frictional force will oppose the downward motion of the screw threads and one must use the following free-body diagram.

One can reverse the axial load W to be pulling the screw out or one can reverse the direction of the screwing moment. These cases can be studied in a similar way. If you need to know how much axial force W or screwing moment M is needed to make the screw turn in a given way, then you assume that the threads are slipping and set . Take the static coefficient of friction if you need the initial value to get the screw started turning, and take the kinetic coefficient of friction if you would like to know what is needed to keep the screw turning.

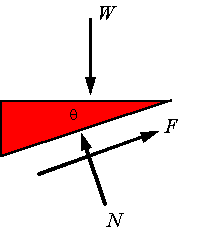
Self-locking screw: A screw is considered self-locking if the lead angle is selected such that in the absence of a screwing moment (i.e., M=0) the frictional force will remain less than so that the threads will not slip relative to each other. This can be studied using the following free-body diagram. The maximum thread angle for the screw to be self-locking is given by setting .