EXAMPLE 3: MASS MOMENT OF INERTIA
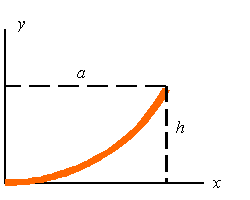
Calculate the mass
moment of inertia of the parabolic rod about the y-axis. Assume the rod is made of a uniform material and has a mass
of m.
Solution:
The
mass moment of inertia about the y-axis
is given by
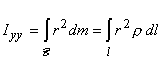
The
length of the bar can be calculated from
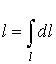

The element of arc
length in a rectangular coordinate system can be written as
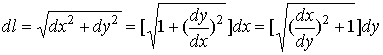
The
equation for the parabola is
![]()
Substitution
of the point (a, h) into this
equation givens the equation of the bar as
![]()
The
length of the bar can, therefore, be calculated as

![]() The distance from the y-axis
is x. Therefore, r=x. The mass moment of inertia about the y-axis can be written as
The distance from the y-axis
is x. Therefore, r=x. The mass moment of inertia about the y-axis can be written as
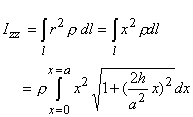
For
a uniform bar the density can be calculated using the total mass and total
length of the bar so that
![]()