Frictionless impact: Impact refers to the interaction of two particles when the interaction interval is very short. Frictionless impact refers to short interactions when there is no noticeable effect due to friction.

 The free-body diagram of the two particles during the collision is

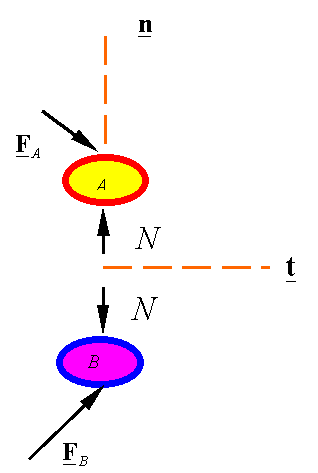
The impulse momentum for each particle is

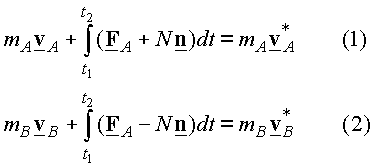
Where and are the externally applied forces. The general impulse momentum relation for this system will be

An empirical relation is used to account for the loss of mechanical energy in the impact. This relation is between the relative speed that the particles approach each other and the relative speed that they separate from each other. This relation is

,

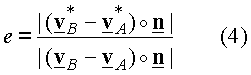where e is the coefficient of restitution, an empirical constant between 0 and 1. The collision is considered elastic if e=1. In an elastic collision the magnitude of the normal component of the relative velocity before and after the collision is the same. The collision is considered fully plastic if e=0. In a plastic collision the normal component of the relative velocity of the two particles becomes zero (i.e., the component of the velocity of the two particles in the normal direction becomes the same).

Note that (3) is a linear combination of (1) and (2), and, therefore, is not an independent equation. Impact problems are solved using equation (4) and a combination of (1), (2), and (3).

When there is negligible impulse due to external forces: The time of the impact is assumed to be small. If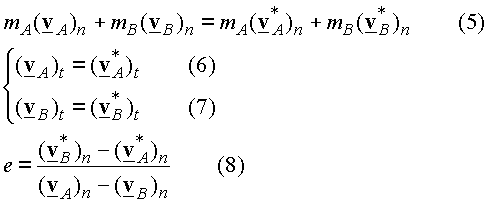 and are bounded (must be less than infinity), when one lets go to zero, the impulse of these forces go to zero and one can simplify the above set of equations to get

The subscripts t and n refer to the components of the vectors along the and directions. Examples of bounded external forces are constant forces, such as the force of gravity, and forces resulting from motion, such as spring forces. In these cases, if the impact time is small, we can ignore the impulse of these forces and use equations (5)-(8).