The linear impulse-momentum relation
Linear momentum of
a particle:
The symbol L denotes the
linear momentum and is defined as the mass times the velocity of a particle.
|
|
|
|
Impulse of a force
from time t1 to t2: The integral of the force
over the time interval of concern is its impulse. The impulse of a force is a
vector given by the integral
|
|
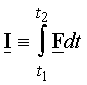
Newton’s 2nd
law:
Newton’s second law states that the resultant of all forces applied on a
particle is equal to the rate of change of linear momentum of the particle.
![]()
This
reduces to the more familiar statement of this law if one notes that in
Newtonian mechanics it is assumed that mass is constant, and, therefore, ![]() .
.
The linear
impulse-momentum relation: Integration of Newton’s 2nd law over the time interval
from t1 to t2 results in
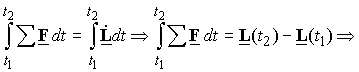
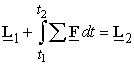
Therefor,
the linear momentum of a particle is changed by the impulse of the resultant
force on the particle. There will be conservation
of linear momentum only if the impulse of the resultant force is zero.
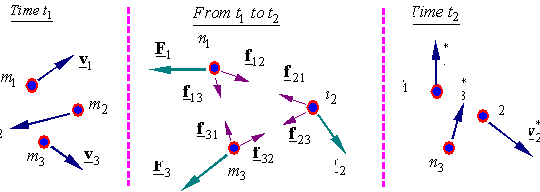
For a system of
particles:
Consider the system of particles shown below. Each particle in the system has a
mass mi and at time t1 has a velocity vi, and from time t1 to time t2 is acted upon by the resultant external force Fi and the internal forces of interaction between
the particles of fij. As a result of the impulse of the internal
and external forces on each particle, at time t2 the particle with mass mi has a velocity v*i.
|
|
Writing
the impulse momentum equation for each particle and adding them up, considering
that Newton’s 3rd law requires that ![]() , we get for n
particles
, we get for n
particles
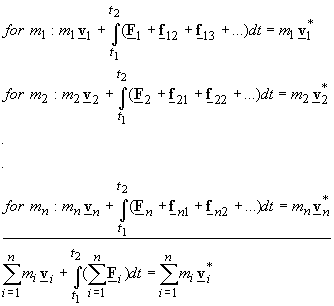
Therefore,
the total linear momentum of the system is changed by the impulse of the
external forces. Recalling the relation ![]() , we can rewrite this equation as
, we can rewrite this equation as
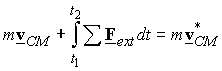
![]()
ã Mehrdad Negahban and the
University of Nebraska, 1996-2002.
All
rights reserved
Copy
and distribute freely for personal use only
Department
of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526