The angular impulse-momentum relation
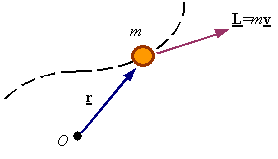
Angular momentum
of a particle:
The symbol HO denotes the angular
momentum and is defined as the moment of linear momentum around the point O, and given by the equation
![]()
|
Impulse of a
moment from time t1 to t2: The integral of the moment
over the time interval of concern is its impulse. The impulse of a moment is a
vector given by the integral
|
|
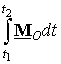
Moment and
rate-of-change-of angular momentum relation: Starting from Newton’s second law,
calculating the moment of both sided of the equation with respect to a point O on an inertial frame results in
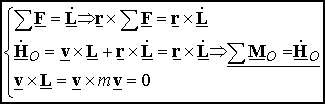
This
resulting relation between the moment and the rate of change of angular
momentum is called the moment-rate of change of angular momentum relation
(MRCAM).
The angular
impulse-momentum relation: Integration of Newton’s 2nd law over the time interval
from t1 to t2 results in


Therefore,
the angular momentum of a particle is changed by the impulse of the resultant
moment on the particle. There will be conservation
of angular momentum only if the impulse of the resultant moment is zero.
![]()
ã Mehrdad Negahban and the
University of Nebraska, 1996-2002.
All
rights reserved
Copy
and distribute freely for personal use only
Department
of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526