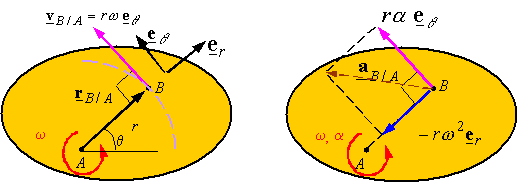Relative motion of points on a rigid body
|
|
Relative velocity
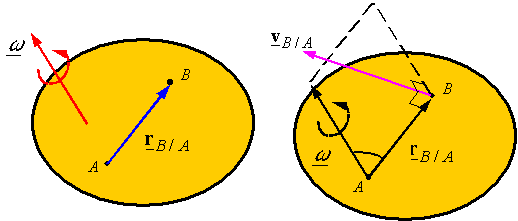
of points on a rigid body: Consider points A and B on a rigid body. The relative position
of B with respect to A is given by rB/A.
The
relative velocity of B with respect
to A is given by 
. Since the distance between points A and B does not change
in a rigid body, |rB/A| is constant and one can
calculate the derivative of rB/A using the lemma to get
where
is the angular
velocity of the rigid body. Since vB/A is the cross product of 
and rB/A, the relative velocity of B with respect to A is
perpendicular to both 
and rB/A.
Relative acceleration
of points on a rigid body: The relative acceleration of point B
with respect to A is given by the
derivative of vB/A. Using the above
expression for relative velocity, one gets
2-D motion: In 2-D, the angular
velocity and angular acceleration can be written as
The
following are graphical representations of the relative velocity and relative
acceleration of points on a rigid body.
|
|
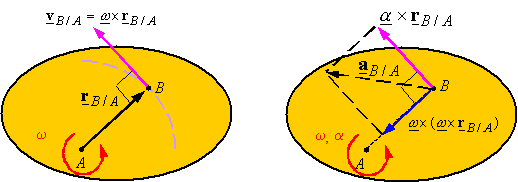
The
left figure shows that the motion of
point B relative to A describes a circle since the distance
between the points does not change. As a result, the velocity of B relative to A is tangent to this circle. The right figure shows the components
of acceleration. Since the relative motion is on a circle, the acceleration of B relative to A has a component tangent to the circle (
= tangential component) and a component towards the center of
rotation (
= centripetal component).
Since
the relative motion of two points on a rigid body always is described by motion
on a circular path, one can also use polar coordinates with a constant radial
coordinate r (i.e., 
), 
, and 
. This results in
expressions for relative velocity and acceleration given as
|
|
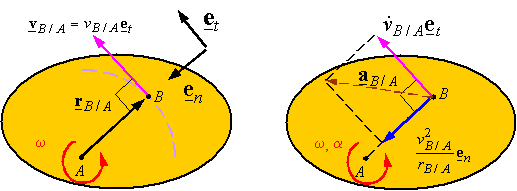
Another
method of describing relative motion is by using normal and tangential
coordinates. This results in
|
|
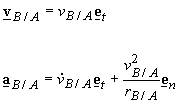
ã Mehrdad Negahban and the
University of Nebraska, 1996-2002.
All
rights reserved
Copy
and distribute freely for personal use only
Department
of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526