Instantaneous Center of Velocity
Extension of a
rigid body:
The extension of a rigid body refers to the operation of theoretically
extending the body to fill all space. By this operation every point in space
becomes a point of the body and as a result has a velocity associated with it.
Since this is not an actual extension of the body, a theoretical extension does
not influence how the actual body moves-it simply follows the motions of the
actual body.
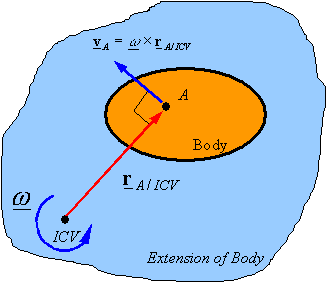
Instantaneous
Center of Velocity (ICV): Any point on a rigid body or on its extension that has zero velocity
is called the Instantaneous Center of Velocity of the body. Assuming one knows
the ICV of a body, one can calculate the velocity of any point A on the body using the equation 
and recognizing that
be definition 
. This gibes
|
|
In
2-D motion, if 
is in the plane of
motion and 
is perpendicular to
this plane, then one can use the scalar relation
Methods of
finding the ICV:
|
|
·
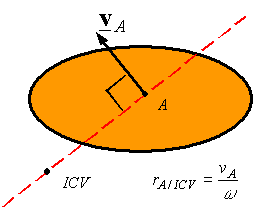
Given
the velocity 
of point A on a rigid body and the angular
velocity of the rigid body one can use the above equation to find the distance 
between the point A and the ICV. One can then draw a line
perpendicular to the velocity and passing through A, and move along this line a distance 
to get to the ICV.
The side on which the ICV is can be determined by the direction of the angular
velocity.
·
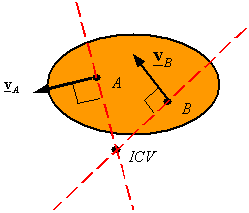
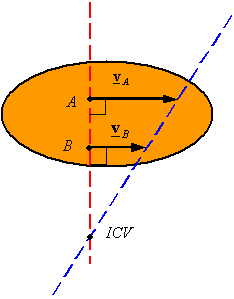
Given
the velocity of points A and B on a rigid body one can find the ICV
by drawing a line perpendicular to 
and passing through A, and by drawing a line perpendicular
to 
and passing through B. One of the following three cases will
result
·
The lines intersect at one point: The point of intersection is the ICV. The
angular velocity can be calculated once the ICV is determined using the
velocity of either point and its corresponding distance from the ICV.
|
|
·
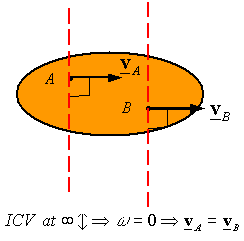
The lines are parallel (they intersect at infinity): The ICV is at infinity, and
the angular velocity is zero since infinity times zero is the only way one can
get velocities other than infinite. Therefore, the body is in pure translation
and the velocity of the two points must be the same.
|
|
·
The two lines fall on top of each other: One can find the location
of the ICV using the proportionality of velocity and distance from the ICV to
create similar triangles. This follows from
|
|
ã Mehrdad Negahban and the
University of Nebraska, 1999-2002.
All
rights reserved
Copy
and distribute freely for personal use only
Department
of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526