Motion relative to moving frames
Two
observers may provide different description of the same event if they are
positioned in different frames. For example, a stationary point on the ground
may look to an observer stationed on a merry-go-round as moving. Or, for
example, passengers sitting in an airplane may consider each other as
stationary, while an observer on earth may consider them to be moving.
Frames: To describe position in
space we use a frame. The frame we use is frequently the background of the
event we are observing, yet we can select any rigid body as our frame to
reference our observations. The earth is the most common frame we use, but it
is not the only one. For example, observations in the shuttle may be done
relative to the “shuttle frame,” and then translated to earth frame.
Time derivatives
and frames:
The derivative of any variable with respect to time provides information on how
it is changing with time. Since the same event when viewed from different
frames may result in different observations, the time derivative of an event
when taken relative to one frame may be different from the time derivative
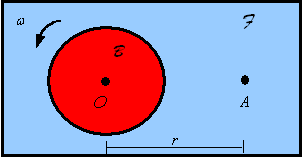
taken relative to another frame. For example, point A which is fixed to frame 
has zero velocity as
seen by an observer on frame , yet will have a downward velocity of 
if observed by an
observer sitting at point O on the
frame 
, which is a disk rotating about O with angular velocity 
relative to .
|
|
One
can relate the time derivative obtained from an observer in one frame to that
obtained from an observer in another frame. Let the vector 
be represent a
quantity being observed by two observers, one on frame and one on frame . Let 
denote the derivative of obtained by the observer on , and let 
denote the derivative
of obtained by the observer on . These derivatives
are related by following equation
|
|
where
is the angular velocity of frame with respect to frame .
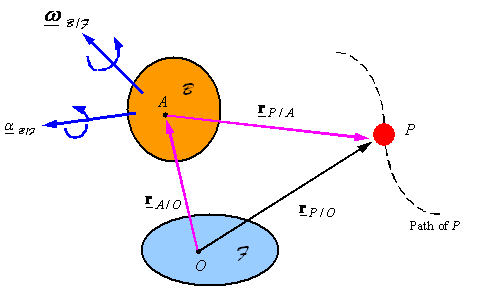
Relating
observations on velocity and acceleration: The position of a point P as it moves on its path can be described relative to the origin O of frame by the position vector
or relative to the
origin A of frame by the position vector
. These vectors are related through the law of vector
addition given by
|
|
Taking
derivatives of both sides of the equation from the point of view of the
observer in and application of the
above relation to relate derivatives in two different frames results in the
relation
The
first term on the right hand side is the velocity as seen by an observer
sitting at point A on frame , the second term on the right hand side is a modification of
this velocity to account for the rotation of frame with respect to , and the third term on the right hand side is a modification
of the first term to account for the translation of with respect to . The derivative of this gives the relation between the
acceleration as observed from the two frames. After application of the rule for
taking derivatives and some reorganization one gets
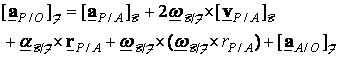
The
first term on the right hand side is the acceleration measured by an observer
located at point A on frame ,
the next three terms are modifications to correct for the rotation of
frame with respect to , and the last term is to correct for the translation of with respect to .
Note: The derivative of is the same in both frames. This follows from
ã
All rights reserved
Copy and distribute freely for personal use only
Department of Engineering Mechanics,
Last modified at: 3:59 PM, Wednesday,
March 26, 2003