Mass moment of inertia
Mass moment of
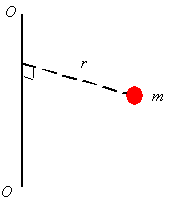
inertia for a particle: The mass moment of inertia is one measure of the distribution of the
mass of an object relative to a given axis. The mass moment of inertia is
denoted by I and is given for a single
particle of mass m as
|
|
where
O-O is the axis around which one is
evaluating the mass moment of inertia, and r
is the perpendicular distance between the mass and the axis O-O. As can be seen from the above
equation, the mass moment of inertia has the units
of mass times length squared. The mass moment of inertial should not be
confused with the area moment of inertia which has units of length to the power
four. Mass moments of inertia naturally appear in the equations of motion, and
provide information on how difficult (how much inertia there is) it is rotate
the particle around given axis.
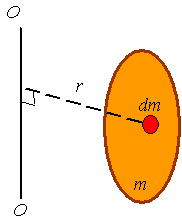
Mass moment of
inertia for a rigid body: When calculating the mass moment of inertia for a rigid body, one thinks
of the body as a sum of particles, each having a mass of dm. Integration is used to sum the moment of inertia of each dm to get the mass moment of inertia of
body. The equation for the mass moment of inertia of the rigid body is
|
|
The
integration over mass can be replaced by integration over volume, area, or
length. For a fully three dimensional body using the density 
one can relate the
element of mass to the element of volume. In this case the density has units of
mass per length cubed and the relation is given as
and
the equation for the mass moment of inertia becomes
The
integral is actually a triple integral. If the coordinate system used is
rectangular then dV=dxdydz . If the
coordinates uses are cylindrical coordinates then 
.
Example 1
For
a two dimensional body like a plate or a shell one can use density 
per unit area (units of mass per length
squared) to change the integration using the relation
where
A is the surface are and dA differential element of area. For
example, for rectangular coordinates dA=dxdy
and for polar coordinates 
. After this substitution one gets the equation to calculate
the mass moment of inertia as
Example 2
If
the body is a rod like object then one can use the relation
to
get
where
l is a coordinate along the length of
the rod and the density 
is in units of mass
per unit length.
Radius
of gyration: Sometime in place of the mass moment of inertia the radius of
gyration k is provided. The mass
moment of inertia can be calculated from k
using the relation
where
m is the total mass of the body. One can
interpret the radius of gyration as the distance from the axis that one could
put a single particle of mass m equal
to the mass of the rigid body and have this particle have the same mass moment
of inertia as the original body.
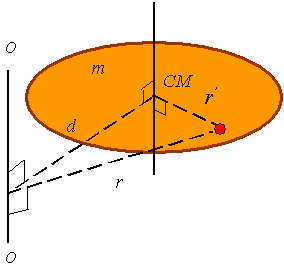
Parallel-axis
theorem: The
moment of inertia around any axis can be calculated from the moment of inertia
around parallel axis which passes through the center of mass. The equation to
calculate this is called the parallel axis theorem and is given as
|
|
where
d is the distance between the
original axis and the axis passing through the center of mass, m is the total mass of the body, and 
is the moment of
inertia around the axis passing through the center of mass.
Composite bodies: If a body is composed of
several bodies, to calculate the moment of inertia about a given axis one can
simply calculate the moment of inertia of each part around the given axis and
then add them to get the mass moment of inertia of the total body.
ã Mehrdad Negahban and the University of Nebraska, 1999-2002.
All rights reserved
Copy and distribute freely for personal use only
Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526