Equations of motion for a rigid body
(Euler’s
laws)
Inertial frame: The explicit form of the
laws of mechanics depend on the frame used to reference the motions. The
reference frame is frequently the background of the event, the earth being the
most common reference frame. For example, Newton’s second law is written as
when
the acceleration 
is calculated
relative to an inertial reference frame. The points of an inertial frame have
no acceleration (purely translating with constant or zero velocity, and no
rotation). On the other hand, this same law will be written as
|
|
if
the acceleration 
is calculated with
respect to a frame which is purely translating with an acceleration of 
. Therefore, it is important to consider the reference frame
carefully before using any particular form of a given law. Most of the time,
the laws of motion are written relative to an inertial frame, then from this
form one can derive the form of the law relative to other frames.
Euler’s laws: The laws of motion for a
rigid body are known as Euler’s laws. Euler gave two laws for the motion of a
rigid body. The two laws written relative to an inertial reference frame are
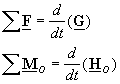
where
O is a fixed point on
the inertial reference frame. The first of Euler’s two laws describes
how the forces control the “translational” motion of the rigid body (i.e., the
change of the velocity of the center of mass, 
). The second of Euler’s two laws describes how the change of
angular momentum of the rigid body is controlled by the moment of forces and
couples applied on the body. The laws of Euler are written for a body of fixed
matter (i.e., matter can not be added to the body, matter can not be subtracted
from the body, nor can matter be replaced by other matter).
An
alternate form of these laws which replaces the need to have a fixed point O on an inertial frame is obtained by
using the center of mass. This law is
derived below and given by
where
CM stands for the center of mass.
A
third alternate form of Euler’s laws can be derived from the second alternate
form. This form replaces the center of mass by an arbitrary
point P which may be moving in
any way (it can be accelerating). This form of Euler’s laws are written as
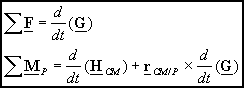
where
is the position of
the center of mass relative to the selected point P. Details of how to obtain this form is also given below. A fourth
form of Euler’s laws is given as
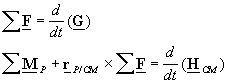
where
is the position of
point P with respect to the center of
mass, and as above P may be selected
arbitrarily.
It
will also be shown that the linear momentum of a rigid body is given by the
mass times the velocity of the center of mass of the body to give the alternate
form of Euler’s first law as
where
m is the total mass of the rigid body
and 
is the acceleration
of the center of mass of the body.
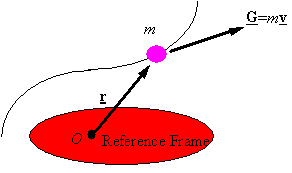
The linear
momentum of a particle: For a single particle of mass m
its linear momentum 
is given by its mass times its velocity so that
The linear
momentum of a body: The linear momentum of a body is assumed to be the sum of the linear
momentum of its “particles”. For example, if one has a body consisting of
several particles each having a mass of 
and a velocity of 
, its linear momentum is given by
|
|
It
is simple to see that for a continuous body the summation can be replaced by
and integration to get
|
|
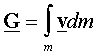
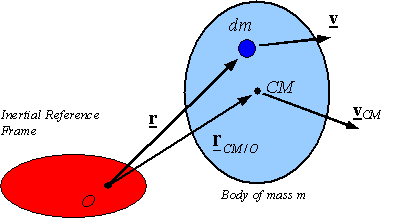
The
location of the center of mass of a body can be found from the relation
Rearranging
this relation and taking its time derivative relative to an inertial frame
yields
where
is the velocity of
the center of mass measured with respect to the reference frame and m is the total mass of the body.
Therefore, one can conclude that the linear momentum of a body is given by
Alternate form of
Euler’s first law: Using the above relation for the linear momentum of a rigid body, one
can replace the linear momentum by the mass times the velocity of the center of
mass to obtain the alternate form of Euler’s first law as
Since
mass is constant in Newtonian mechanics, one arrives at the relation
Note: For a single particle the
center of mass and the location of the particle are the same and one recovers
Newton’s second law.
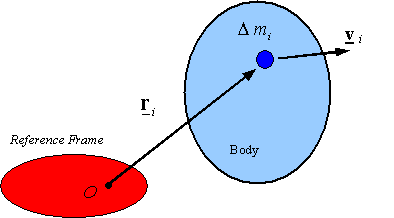
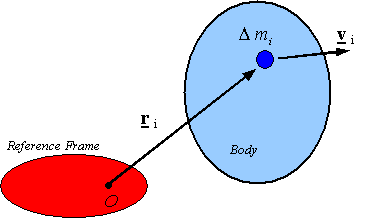
Angular momentum
of a particle:
The symbol HO denotes the angular
momentum and for a particle of mass m
is defined as the moment of linear momentum around the point O, and given by the equation
|
|
Angular momentum
for a rigid body: The angular momentum for a rigid body is the sum of the angular
momentum for the “particles” in it. Given a reference frame, a point O on this reference frame, and a rigid
body, one can approximate the angular momentum
of the rigid body as
|
|
where
the body is assumed to be approximated by a sum of parts, each having a mass 
, a position 
, and a velocity 
.
Taking
a limit as the parts get smaller brings one to the following integral
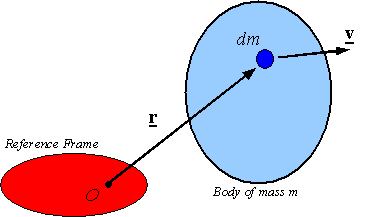
representation of the angular momentum of a rigid body
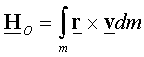where
m is the total mass of the body and 
and 
are, respectively,
the position and velocity of dm
relative to the selected reference frame and the selected reference point O on it.
|
|
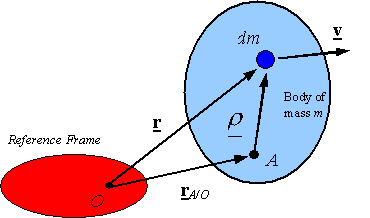
The relation
between moments of forces when the moment is taken about different points: The moment of a force taken
about O can be related to the moment
of the same force taken about point A
by the relation
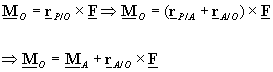
The relation
between angular momentums when the angular momentum is taken about different
points: The
angular momentum of a body taken about O
can be related to the angular momentum of the same body taken about point A by the relation
|
|
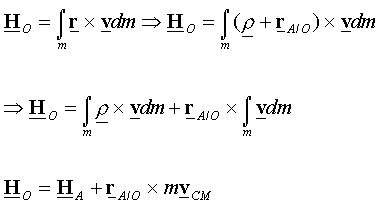
Alternate forms
of Euler’s second law: A useful alternate form to Euler’s second law can be obtained by using
the above change of reference point rules to write the second law as
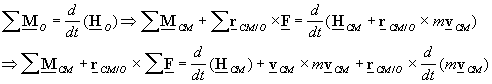
Taking
advantage of the Euler’s first law, and noting that the second term on the
right hand side is zero, one gets the alternate form of Euler’s second law as
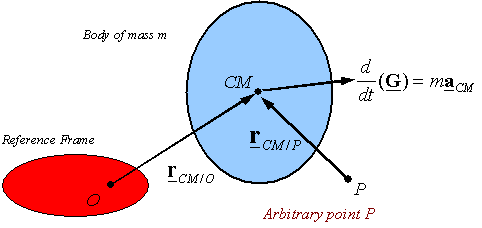
The
importance of this form is that the moment and the angular momentum are
calculated relative to the center of mass, which need not be on an inertial
frame. Therefore, the need to use a selected point O on an inertial frame has been removed in favor of the center of
mass that may be accelerating. Taking the moment of Euler’s first law around an
arbitrary point P and adding it to
this equation results in
One
can rewrite this in one of the two other alternate forms
|
|
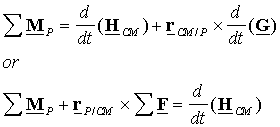
ã Mehrdad Negahban and the University of Nebraska, 1999-2002.
All rights reserved
Copy and distribute freely for personal use only
Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526