Rectilinear
Motion
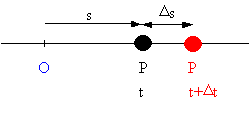
Time: t
Position: s
Speed: v
Acceleration: a
Lemma:
Method for integration:
1. Check
to see if there are only two variables
2. If
you have only two variables, see if you can separate the variables (SV)
3. If
you have more than two variables or if your variables are not the ones you are looking
for, use the lemma to see if you can work around the problem
4. Once
you have separated the variables, then integrate (I)
Acceleration as a function of time: a=f(t)
C and D are constants of integration evaluated
from initial conditions
Acceleration as a function of velocity: a=f(v)
If you can solve to get v=k(t), then
or by using the lemma
Acceleration as a function of position: a=f(s)
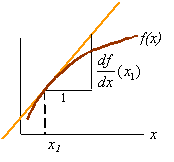
Derivatives to know:
The chain rule for derivatives:
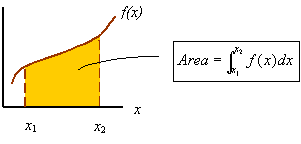
Integrals to know:
Change of variables: Given a function U(x), one can use 
to change the
variable of integration from x to U for an integral of the form
Integration by parts:
ã Mehrdad Negahban and the
University of Nebraska, 1999-2000.
All
rights reserved
Copy
and distribute freely for personal use only
Department
of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526