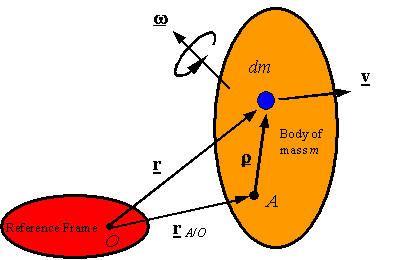
Calculating angular momentum for a rigid body

Alternate forms for calculating angular momentum: A useful expression for calculating the angular momentum is based on introducing a point A fixed to the body and using the kinematic relations

where is the angular velocity of the body as seen by an observer on the reference frame. Introducing these relations into the expression for the angular velocity yields the expression

Angular momentum of a body rotating around a fixed point on the reference frame: If the body is pinned or ball and socket connected to the reference frame at O, then one can simplify the above expressions by taking A equal to O to get

Using an arbitrary intermediate point A on the rigid body: If A is an arbitrary point on the rigid body, one can use the relation

to get

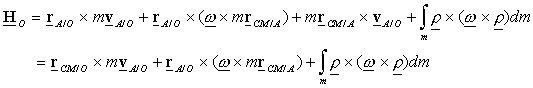
Using the intermediate point A as the center of mass: If one sets A as the center of mass, then the expression for the angular momentum about O becomes

Since the mass of the body is “evenly” distributed around the center of mass, one can conclude that

Therefore, one obtains the expression for angular momentum about an arbitrary point O as

Note: in all the above expressions for angular momentum an integral needs to be calculated of the form

A general expression for this can be found by selecting

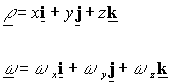
and directly calculating the integral to get

where the moments of inertia are given by

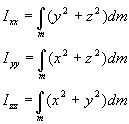
and the products of inertia are given by

ã Mehrdad Negahban and the University of Nebraska, 1996-2002.

All rights reserved

Copy and distribute freely for personal use only

Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0347