Eulerís
second law for 2-D motion
Two-dimensional
motion: A
three dimensional body is considered to be in two dimensional motion if the
direction of its angular velocity does not change with time. If in an (x,y,z) coordinate system the direction
of the angular velocity is in the z-direction,
then for a two dimensional motion one can write
![]()
where
![]() †and
†and ![]() †are, respectively,
the angular velocity and angular acceleration of the rigid body relative to an
inertial frame. Each particle of a body in two-dimensional motion will be
moving on a plane.
†are, respectively,
the angular velocity and angular acceleration of the rigid body relative to an
inertial frame. Each particle of a body in two-dimensional motion will be
moving on a plane.
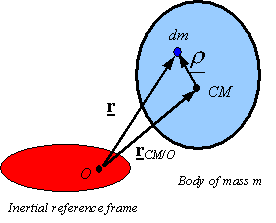
Angular momentum: There are several
expressions for calculating angular momentum. First consider calculating the
angular momentum relative to a fixed point O
on an inertial reference frame. For this case one can use the relation
![]()
where
![]() †is the position of dm relative to the center of mass.
†is the position of dm relative to the center of mass.
|
|
To
calculate the integral one needs to calculate its argument first. This can be
done as follows
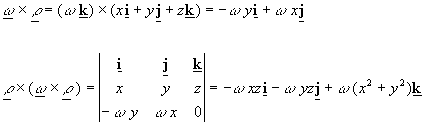
Substituting
into the above yields
![]()
where
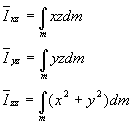
are
the products of inertia and moment of inertia about
the center of mass.
It
is easy to see by inspecting this equation that if one replaces the CM for point O,† that the angular
momentum about the center of mass can be obtained as
![]()
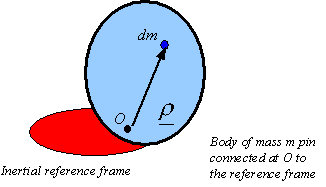
If O is a point on the body which is fixed
to the inertial reference frame (pin connected), then the moment of inertial of
about O can be directly calculated as
![]()
where
the products and moment of inertial are now calculated relative to axis passing
through the fixed point O.
|
|
Rate of change of
angular momentum: When taking the time derivative to obtain the rate of change of
angular momentum one needs to be in an inertial reference frame. Let† F be an inertial reference
frame and B be the rigid body. If the (x,y,z) coordinate axis is fixed to the rigid body, the base vectors
and the moments and products of inertial will be constant relative to the rigid
body. Using the general kinematical rule for taking derivatives
![]()
one
will obtain
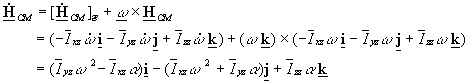
Using
the relation
![]()
one
obtains the equation for the derivative with respect to time of the angular
momentum with respect to a point O on
an inertial frame as
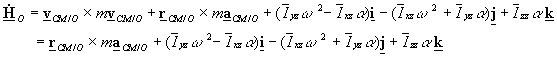
If O is a point on the rigid body fixed to
an inertial frame (pinned connected), then one will get
![]()
Note: The products of inertia Ixz and Iyz are a measure of how balanced the body
is. If the body is balanced, then the products of inertia will be zero. In case
of a plate like body, where the z-coordinate
of all points is zero, then the products of inertia will also be zero. In the
case that the products of inertia are zero the rate of change of angular
momentum will only have a z-component.
†
Eulerís 2nd
law for 2-D motion: The following are some variations of Eulerís second law for a rigid
body. They all follow from previously derived relations.
∑
For
any general two dimensional motion:
![]()
∑
For
any general two dimensional motion where P
is any arbitrary point and O is a
point on an inertial reference frame:
![]()
∑
For
a rigid body pinned to an inertial frame at O:
![]()
Note: In general only the z-component of these equations are used.
The other two components represent the moments needed to keep an unbalanced
body in two dimensional motion (i.e., keep the direction of the angular
velocity from changing). If the body is properly balanced so that the products
of inertia are zero, then these components of the rate of change of angular
momentum go to zero and, therefore, zero moment is needed to keep the body in
two dimensional motion (i.e., if a balanced body is put in two dimensional
motion, it will remain in two dimensional motion until moments are applied
around the x- and/or y-axis to change this).
![]()
„ Mehrdad Negahban and the University of Nebraska, 1999-2002.
All rights reserved
Copy and distribute freely for personal use only
Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526