Work-Energy relation for a rigid body
Work of a force: One calculates the work of
a force on a rigid body exactly the same as one would calculate the work of a
force for a particle. For a rigid body, the velocity used is the velocity of
the particle on the rigid body that the force is applied on.

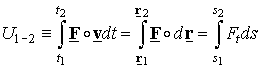
Power of a
couple: The
power of a couple M applied
on a rigid body having an angular velocity of ![]() is given by
is given by
![]()
Work of a couple: The work of a couple is the integral of its power over a time.
Work of a couple
in 2-D: The
work of a couple applied on a rigid body in two-dimensional motion is
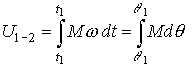
Kinetic energy of
a rigid body:
The kinetic energy of a rigid body can be evaluated from one of the following
equations
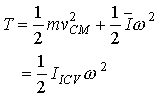
Work-Energy
relation: The work energy relation for
a rigid body is given as
![]()
As
for a particle, one can use the potential energy to calculate the work of
conservative forces and use the alternate form of the work-energy relation
given by
![]()
Potential energy: The potential energy for a
constant gravitational acceleration is given by
![]()
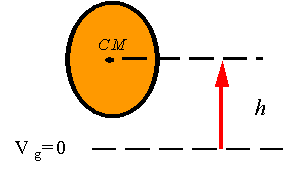
where h is measured from a reference elevation
to the center of mass of the rigid body.
The potential energy of a spring is calculated exactly the same as
for a particle so that
![]()
where k is the spring
constant, l is the current length, lo is the free length.
![]()
ã Mehrdad Negahban and the
University of Nebraska, 1999-2002.
All
rights reserved
Copy
and distribute freely for personal use only
Department
of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526