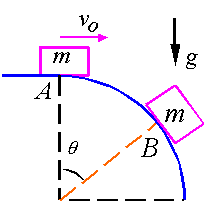
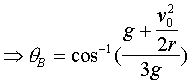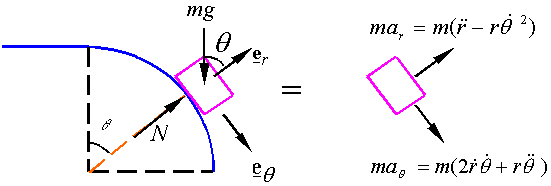EXAMPLE 4: Newton’s 2nd law
|
|
A particle starts at A with an initial velocity of ![]() , and moves down the smooth circular ramp up to point B when
it separates. Obtain the equation of
motion of the particle and the angle
, and moves down the smooth circular ramp up to point B when
it separates. Obtain the equation of
motion of the particle and the angle ![]() at which it
separates.
at which it
separates.
Solution:
|
|
Kinematics:
r = constant
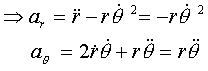
Kinetics:
![]()
![]()
(2) is the equation
of motion
At point of separation, N=0
![]()
Integrating (2) using
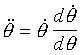
we get
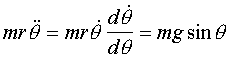
![]()
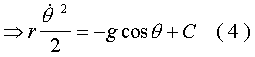
By the initial conditions at A
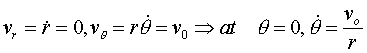
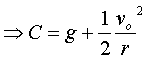
Substitution of C into (4) gives
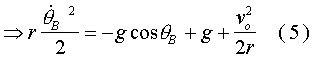
Solving for ![]() and substituting into
(3) gives
and substituting into
(3) gives