How Materials Carry Load
Basic
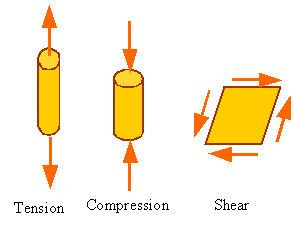
modes of loading a material: Tension, compression and shear
Stress:
Loads applied on a material are distributed over a surface. For example, the point load shown in the following figure might actually be a uniformly distributed load that has been replaced by its equivalent point load.
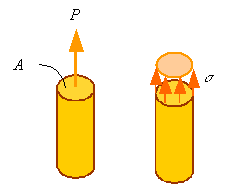
Stress is the load applied per unit
area of the surface it is applied on. Normal stress is
the stress normal to a surface and is denoted by the symbol "![]() " (sigma). In the above
figure the normal stress is uniform over the surface of the bar and is given by
" (sigma). In the above
figure the normal stress is uniform over the surface of the bar and is given by
![]()
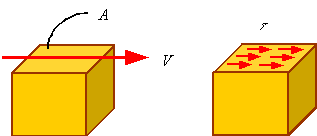
Shear
stress is the stress tangent to a surface. If in the following figure
the shear stress ![]() (tau) that results in the shear load V is uniformly distributed over the
surface, then the shear stress can be calculated by dividing the shear force by
the area it is applied on.
(tau) that results in the shear load V is uniformly distributed over the
surface, then the shear stress can be calculated by dividing the shear force by
the area it is applied on.
![]()
The units of stress are the units of load divided by the units of area. In the SI system the unit of stress is "Pa" and in the U.S. system it is "Psi". Pa and Psi are related to the basic units through the following relations
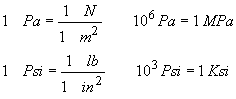
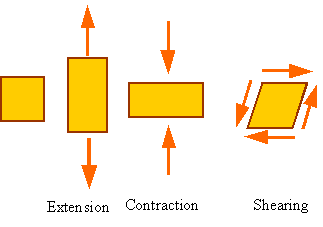
Basic modes of
deformation of a material: Extension, contraction, shearing
Material element can be extended, compressed, or sheared. The following figure shows how the square section to the left changes its shape during extension, contraction and shearing.
Strain:
Strain is the way engineers represent the distortion of a body. Axial strain (normal strain) in a bar is a measure of the extension of a bar per unit length of the bar before deformation. The following figure shows a bar of initial length lo that is extended by the application of a load to the length l.

The axial strain, denoted by ![]() (epsilon), in a homogeneously deforming bar is
calculated by dividing the amount the bar extends by its initial length. This
yield the equation
(epsilon), in a homogeneously deforming bar is
calculated by dividing the amount the bar extends by its initial length. This
yield the equation
![]()
A positive axial strain represents extension and a negative axial strain represents a contraction. Strain has no units since it is one length divided by another length.
Shear strain, denoted by ![]() (gamma), is a measure of how the angle between
orthogonal lines drawn on an undeformed body changes with deformation. In the
following figure the square has been sheared into a parallelogram.
(gamma), is a measure of how the angle between
orthogonal lines drawn on an undeformed body changes with deformation. In the
following figure the square has been sheared into a parallelogram.
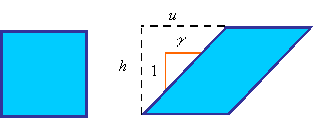
The shear strain is calculated from the equation
![]()
As can be seen from the following figure, the shear strain is equal to the tangent of the change in angle or the two orthogonal sides.
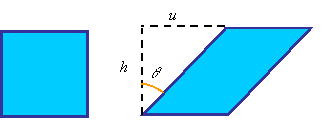
![]()
The difference between ![]() and
and ![]() becomes less and less
as the angle
becomes less and less
as the angle ![]() (in radians) becomes
small. This is since the tangent of an angle, given in radians, can be
approximated by the angle for small values of the angle. In most structural
materials the shearing is small and we can use the approximation
(in radians) becomes
small. This is since the tangent of an angle, given in radians, can be
approximated by the angle for small values of the angle. In most structural
materials the shearing is small and we can use the approximation
![]()
Tensile
behavior different materials:
In a typical tensile test one tries to induce uniform extension of the gage section of a tensile specemin. The gage section of the tensile specimine is normally of uniform rectangular or circular cross-section. The following figure shows a typical dog-bone sample. The two ends are used for fixing into the grips, which apply the load. As can be seen from the free-body diagram to the right, the load in the gage section is the same as the load applied by the grips.
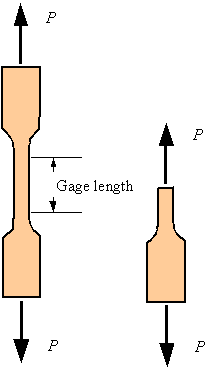
Using extensometers to measure the change of length in the gage section and a load cells to measure the load applied by the grips on the sample one calculates the axial strain and normal stress (knowing the initial gage length and cross-sectional area of the gage section). The result is a stress-strain diagram, a diagram of how stress is changing in the sample as a function of the strain for the given loading. A typical stress-strain diagram for a mild steel is shown below.
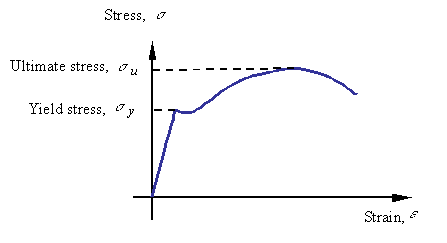
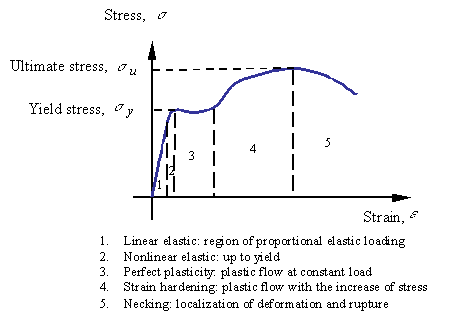
The different regions of the are response denoted by their characteristics as follows
Brittle
versus Ductile behavior:
Brittle materials fail at small strains and in tension. Examples of such materials are glass, cast iron, and ceramics. Ductile materials fail at large strains and in shear. Examples of ductile materials are mild steel, aluminum and rubber. The ductility of a material is characterized by the strain at which the material fails. An alternate measure is the percent reduction in cross-sectional area at failure.
Different types of response:
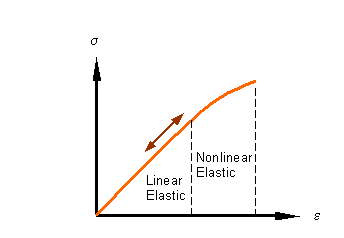
Elastic
response:
If the loading and unloading stress-strain plot overlap each other the response is elastic. The response of steel below the yield stress is considered to be elastic.
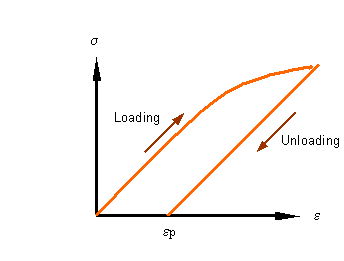
Elastic-plastic
response:
After loading beyond the yield
point, the material no longer unloads along the loading path. There is a
permanent stretch in the sample after unloading. The strain associated with
this permanent extension is called the plastic strain (![]() on the figure). As shown in the figure, the unloading path
is parallel to the initial linear elastic loading path.
on the figure). As shown in the figure, the unloading path
is parallel to the initial linear elastic loading path.
Viscoelastic
response:
Most plastics when loaded continue to deform over time even without increasing the load. This continues extension under constant referred to as creep. If held at constant strain, the load required to hold the strain decreases with time. The decrease in load over time at constant stretch is referred to as relaxation.
Even though bearing
stress is not a fundamental type of stress, it is a useful concept for the
design of connections in which one part pushes against another. The compressive
load divided by a characteristic area perpendicular to it yields the bearing
stress which is denoted by ![]() . Therefore, in form, the bearing stress is no different from
the compressive axial stress and is given by
. Therefore, in form, the bearing stress is no different from
the compressive axial stress and is given by
![]()
where F is the compressive load and A is a characteristic area perpendicular to it.
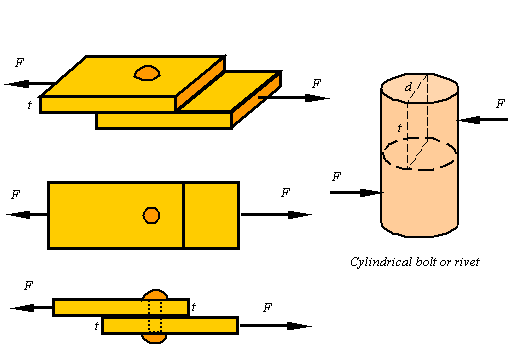
For example, if two plates are connected by a bolt or rivet as shown, each plate pushes against the side of the bolt with load F. It is not clear what the contact area between the bolt and the plate is since it depends on the size of the bolt and the shape of the deformation that results. Also, the distribution of the load on the bolt varies from point to point, but as a first approximation one can use the shown rectangle of area A=td to get a representative bearing stress for the bolt as
![]()
![]()
ã Mehrdad Negahban and the
University of Nebraska, 1996-2000.
All rights reserved
Copy and distribute freely
for personal use only
Department of Engineering
Mechanics, University of Nebraska, Lincoln, NE 68588-0526
Last modified at: 3:07 PM, Wednesday, August 30, 2000