Extension of bars

Uniform bars:

Consider the problem of calculating the extension due to the application of an axial load P on a uniform bar as shown in the figure.

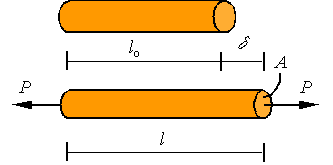
A bar is considered uniform if its cross-sectional area and elastic modulus are constant along the length of the bar. For such a bar under axial loading, the stress and strain along the bar are constants and given by the expressions

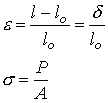
Assuming small strains and substituting these expressions into Hooke’s law , one arrives at the equation for the extension of the bar given as

Non-uniform bars:

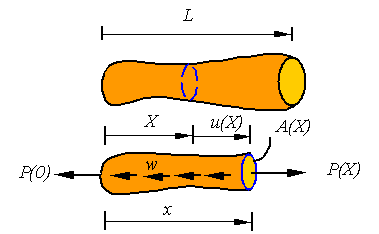
A bar with a varying cross-sectional area is an example of non-uniform bar. In general, one can have varying cross section, elastic modulus, and axial load in a bar. Such situations may result in varying stress and strain along the bar. This, in turn, requires a more in depth analysis to evaluate the extension of the bar. First, let us setup the kinematics of the deformation. As shown in the figure, in a typical situation one would have an initial unloaded configuration (top) and a configuration after loading (bottom).

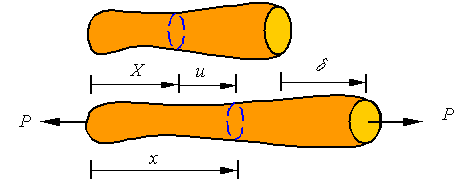
A typical cross-section that is at location X in the initial configuration, ends up in location x in the current configuration by being displaced a distance u from its original location. Each cross section can be displaced a different amount and may have a different cross-sectional area. Therefore, the displacement and cross-sectional area are each a function of the location along the bar (i.e., u(X) and A(X)). A typical segment of length of the bar is shown in the following figure.

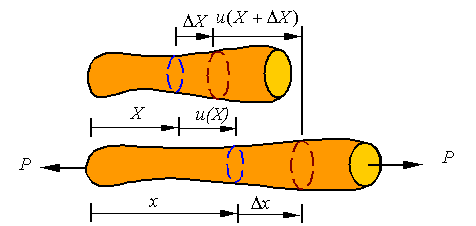
The average strain in this segment of the bar is given by the expression

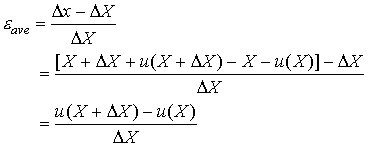
One can take a limit as goes to zero to define the strain at each point of the bar by

The extension of any segment of the bar is the difference between the displacement of one end minus the displacement of the other end. This expression for strain can be integrated to get the extension. Let us say we are looking for the extension of the segment between X₁ and X₂. This would be given by integrating the strain to get

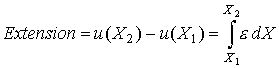
The total extension of a bar of initial length L is given by the expression

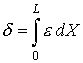
As shown in the figure below, the bar might have a distributed load w applied on it in addition to point loads. As a result, the load and cross-sectional area might both vary with location in the bar so we will denote the load in the section at X by P(X) and the cross-sectional area by A(X). Therefore, the axial stress is given by

Since the material can change along the bar, the elastic modulus may also be a function of location along the bar. From Hooke’s law it follows that the strain at each point of the bar is given by

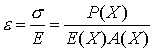
Therefore the total extension in a non-uniform bar is given by

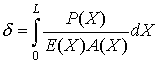
This expression reduces to the one for a uniform bar when the argument of the integral is constant.

ã Mehrdad Negahban and the University of Nebraska, 1996-2000.

Copy and distribute freely for personal use only

Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526

Last modified at: 5:56 PM, Wednesday, August 23, 2000