Thermal Strain
Linear coefficient of thermal
expansion:
An unloaded uniform bar will extend due to a uniform
change in the temperature. This extension ![]() is linearly
proportional to the temperature change and the strain associated with it is
given by the relation
is linearly
proportional to the temperature change and the strain associated with it is
given by the relation
![]()
where ![]() is the linear coefficient of thermal expansion and
is the linear coefficient of thermal expansion and ![]() is the rise in
temperature.
is the rise in
temperature.
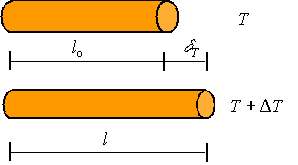
The strain is given by the extension divided by the
original length through the standard relation
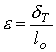
Combining this and the above expression one gets the
relation for the extension of a uniform bar under a uniform change in
temperature as
![]()
For a non-uniform bar or a non-uniform temperature
distribution in the bar, one needs to integrate the strain using the expression
for extension of a non-uniform bar to get

Volumetric coefficient of thermal
expansion:
The volumetric strain ![]() is linearly
proportional to the change in temperature and is given by the relation
is linearly
proportional to the change in temperature and is given by the relation
![]()
where the coefficient of proportionality ![]() is the volumetric coefficient of thermal expansion.
is the volumetric coefficient of thermal expansion.
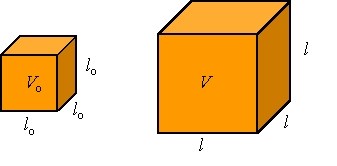
The volumetric coefficient of thermal expansion is related to the linear coefficient of thermal expansion through the
relation between the volumetric strain and the axial strain. The volumetric
strain e is given as the change in volume divided by the original volume
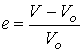
For a cube of isotropic material (a material which behaves
the same along all different directions) with initial sides of length lo,
the initial volume is ![]() and since each side
extends an amount
and since each side
extends an amount ![]() , the new volume is
, the new volume is ![]() . Substituting these expressions into the above relation one
gets for small thermal strains the approximate relation
. Substituting these expressions into the above relation one
gets for small thermal strains the approximate relation
![]()
Therefore, for small thermal strains in an isotropic
material the relation between the linear coefficient of thermal expansion and
the volumetric coefficient of thermal expansion is given by
![]()
Combining thermal and mechanical
loads:
Since
we only are considering linear theories, it is assumed that the thermal and
mechanical effects are additive in the sense that the total strain ![]() in a bar is the
addition of the thermal strain
in a bar is the
addition of the thermal strain ![]() and the mechanical strain
and the mechanical strain
![]() . For a uniform bar under both uniform thermal and mechanical
loading, this can be written as
. For a uniform bar under both uniform thermal and mechanical
loading, this can be written as
![]()
which
results in the total extension being given by
![]()
In the case of non-uniform members, one simply integrated
the expression for strain once for the thermal strain and then again for the
mechanical strain to get, respectively, the expression for the extension due to
thermal expansion and the expression for the extension due to mechanical
loading. Again, the sum of these expressions is the total extension of the bar
![]()
ã Mehrdad Negahban and the University of Nebraska, 1996-2000.
All rights reserved
Copy and distribute freely for personal use only
Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526
Last modified at: 4:18
PM,
Thursday, August 31, 2000