TORSION
Basic
kinematics of torsion:
It
is assumed that when twisted each cross-section in a circular bar rotates as a
rigid body. If the amount of rotation of each cross-section is given by the
function 
, the total twist 
in the bar of length l
shown is given
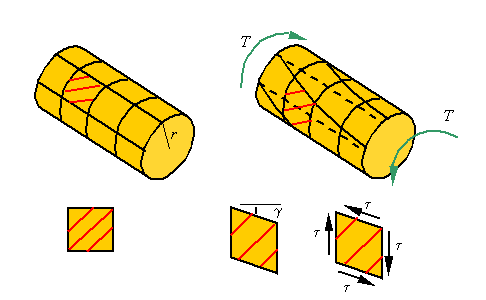
During
the torsion of a bar, axial lines drawn on the surface of a bar become helical
and circumferential lines remain circumferential. Therefore, as can be seen in
the figure, material elements are sheared in the process. This shear strain
must be accompanied by a shear stress (from Hook’s law we know
).
The
shear strain can be related to the rotation of the cross sections. If over an
increment of length 
, the cross section rotates an amount 
, then as can be seen in the figure the shear strain is given
by
Therefore, at the limit one can write
As a result, the shear strain starts at zero at the center and reaches a maximum at the outer radius.
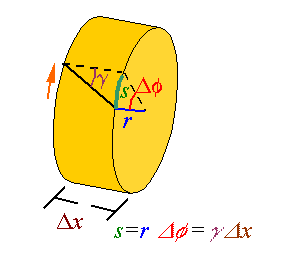
The shear stress:
The shear
stress, through Hook’s law, is related to the shear strain. Therefore, the
shear stress is given by
Again, like the
shear strain, the shear stress is zero at the core of the bar and increases
linearly to a maximum at the outer surface.
Calculating the
torque from the shear stress:
The torque transmitted through the cross-section of a bar is the resultant of the moments created by the shear stresses on the cross-section.
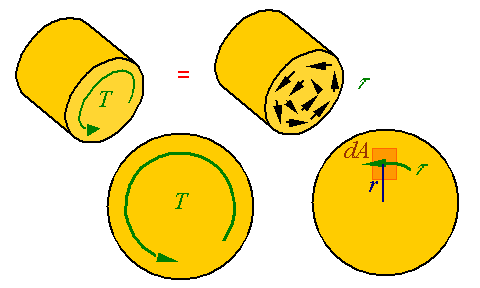
The differential shear load dV
that results from the shear stress applied over the area dA of the cross
section is 
. The moment created by such a shear load is dM = rdV.
The equivalent torque T on the cross section is the resultant of all the
moments crated by the shear stresses so that
Using the expression for shear stress in
terms of twist in the bar we get
where Ip is the polar
area moment of inertia of the cross section. Using this relation, the
expression for shear stress in terms of the torque follows from
Total twist in
a bar:
The total twist in a bar is given by
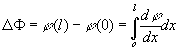
The twist per unit length in terms of
the torque is given by
Therefore, the total twist can be
calculated from
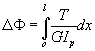
In the case of a uniform bar for which the 
is constant one can move the argument out and integrate to
get
ã Mehrdad Negahban and the University of Nebraska, 1996-2000.
All rights reserved
Copy and distribute freely for personal use only
Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526