PURE SHEAR and POWER TRANSMISSION

 

Pure shear: Consider the material element loaded in pure shear as shown in the figure

 

 

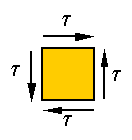
Stress on an inclined plane in this element is neither pure shear nor pure tension, it is a combination of both. Let  and  denote, respectively, the shear and normal stresses on the surface that makes an angle  with the vertical, as shown in the following figure.

 

 

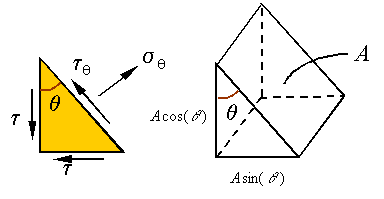
One can use equilibrium to calculate these stresses. If the area of the inclined surface is A, then the area of the vertical surface will be  and the area of the horizontal surface will be , as shown in the above figure. The load on each surface can be calculated using the stresses and the areas they are applied on. Therefore, the free-body-diagram can be drawn as follows.

 

 

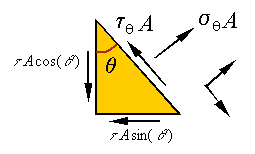
The sum of forces along the incline yields

 

 

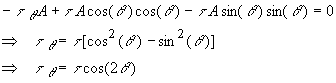
The sum of forces along the normal to the incline yields

 

 

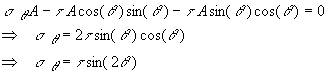
As can be seen from these equations, the maximum shear stress  is  and occurs when  or in other words when

 

 

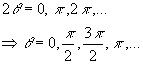
Note that these surfaces are the original vertical and horizontal surfaces on which the pure shear was applied. The maximum normal stress is and occurs when  or in other words when

 

 

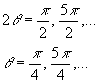
The minimum normal stress is and occurs when  or in other words when

 

 

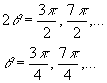
Note that the maximum and minimum normal stresses occur on surfaces which are 90o from one and other, and which are 45o from the vertical and horizontal lines. Also, note that the shear stress is zero at the angles where we have the maximum and minimum normal stresses. One can draw this on a diagram representing the stress on an element that is cut from the original as follows

 

 

 

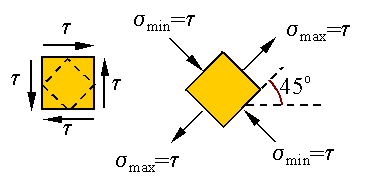
Since in torsion material elements that have sides that are along and perpendicular to the axis of the bar are subjected to pure shear, we can conclude that the surfaces of maximum tensile stress scribes a 45o helix  as shown below.

 

 

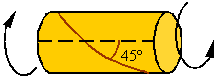
Ductile materials fail in shear and, therefore, a shaft made from a ductile material and under torsion will have a break surface that is perpendicular to the axis of the bar. Brittle materials fail in tension and, therefore, a shaft made of a brittle material and under torsion will break on a surface that is in the shape of a 45o helix as shown above.

 

Strain in pure shear:

 

As shown above, the state of stress described as pure shear can be replaced by a state of stress that is a combination of tension and compression as follows

 

 

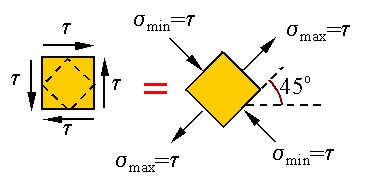
Let us consider a linear elastic material. Since the theory is linear, we can consider the following equivalence

 

 

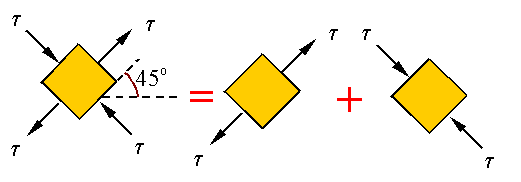
Therefore, the strains can be calculated based on the superposition of those resulting from the tension and compression. If the square originally has sides of length a, then we will have

 

 

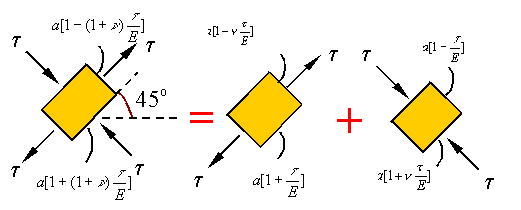
where  we have used Hooke's law for calculating the stretch along the axis of the load in each of the uniaxial extensions and we have used Poisson's ratio to calculate the transverse strain. Let us now look at how the shear and extension are related. Take e to denote the total axial strain given by

 

 

The following figure shows the deformation of both the original pure shear element and the 45o element. In this figure q gives the angle of shear which for small strains is approximately equal to the shear strain g.

 

 

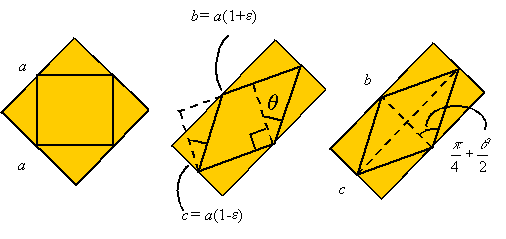
From the figure we can see that

 

 

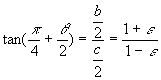
We can expand the tangent function using the identity

 

 

Assuming small angle q, we get the

 

 

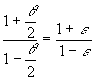
For small angles we know that , so that we get

 

 

This relation can be used to relate the shear modulus to the elastic modulus and Poisson ratio since we can substitute e from above into the equation and use Hooke's law for shear to get

 

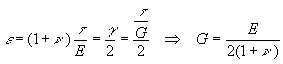
Note that this expression states that the shear modulus, the elastic modulus, and Poisson's ratio are not independent. One can calculate the third given any two.

 

Transmission of power:

 

Power is the rate at which work is being done. If P denotes power and W denotes work, then the relation between power and work can be written as

 

 

The torque T applied on a shaft rotating with an angular velocity w has a power given by the expression

 

 

 

In this expression the angular velocity is in radians per unit time. The angular velocity is related to the frequency f by the relation

 

 

Therefore, one can write

 

 

Power can be given in terms of horsepower by the expression

 

 

where n is in rpm (rounds per minute) and T is in lb-ft.

 

The work done by a constant torque over a given time interval can be calculated by integrating the power to get

 

 

In this expression  is the total angle of rotation over the given time interval.

 

 


ã Mehrdad Negahban and the University of Nebraska, 1996-2000.

All rights reserved

Copy and distribute freely for personal use only

 

Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526