Stress-element and plane stress

General stress state at a point:

At each point in a loaded material body the stress can be characterized by a stress element which shows the shear and normal stresses on a cube. The figure shows such an element taken from a body under three dimensional loading.

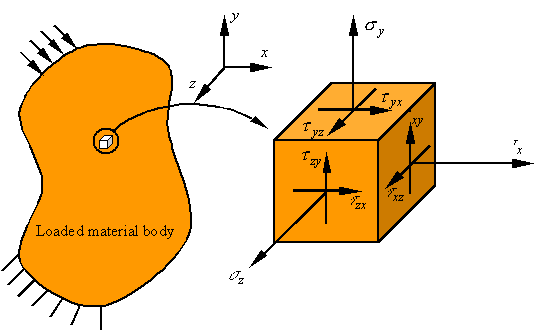
The first subscript on the shear stress denotes the normal to the surface on which the shear stress is applied, and the second index refers to the direction of the shear stress. It can be shown that the “stress is symmetric,” meaning that

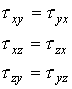
Plane stress:

The state of stress referred to as plane stress is characterized by one surface being free of traction. Taking the surface with normal along the z-direction to be the free surface, the state of stress for plane stress can be drawn as follows.

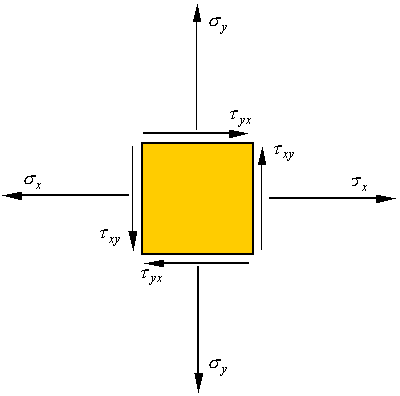
Stress on an inclined surface in stress:

Consider the plane stress element shown. If a section from this element is separated as shown, the normal and shear stress on this surface can be calculated by the following process.

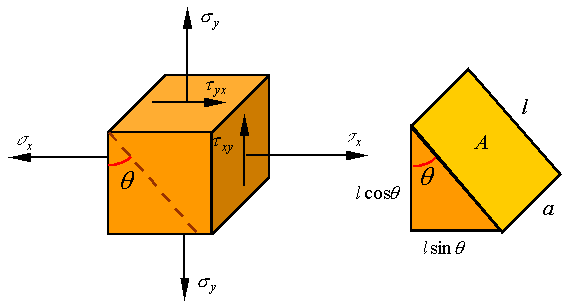
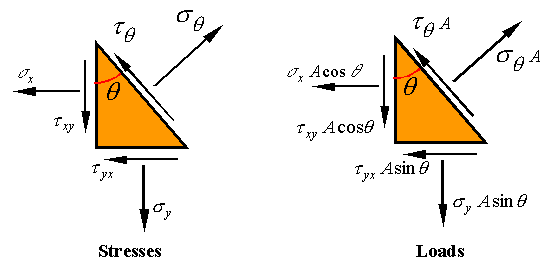
If the area of the surface exposed by the cut is A, then the area of the surface to the left will be and the area of the surface at the bottom will be . The stresses on these surfaces are shown on the left below, and the load on the surfaces (stress times area) are shown on the right below.

Equilibrium of forces in the direction normal to the inclined surface requires that

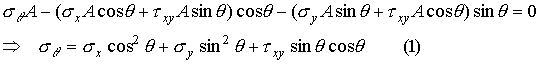
where we have used the fact that stress is symmetric to replace by . Equilibrium in the direction tangent to the inclined surface requires that

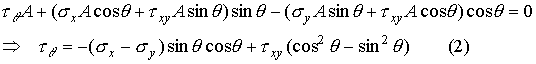
One can use the following trig identities to reorganize these expressions.

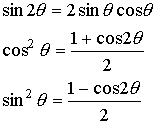
The result of using these identities is

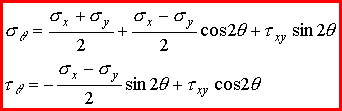
Elements selected along different coordinate directions:

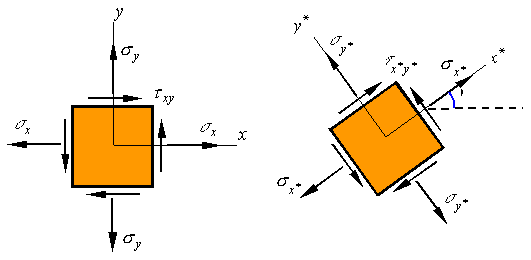
If in place of the x-y coordinate system the stress element is oriented along the x^*-y^* coordinate directions, the normal and shear stresses on the element will look as follows.

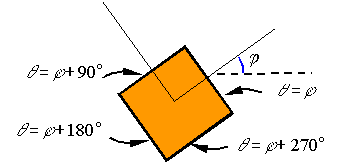
This new coordinate system is rotated an angle counter-clockwise from the original system. Each surface of this new element is an inclined surface for which one can calculate the stresses using the above equations. Note that the orientation of each of the four surfaces are given below.

Substitution of these angles into the equations for normal and shear stress on inclined surfaces results in

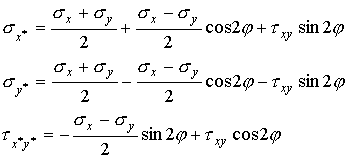
Note that the sum of the two normal stresses results in the relation

which states that the sum of the two normal stresses on a stress element should be the same irrespective of the coordinate directions selected.

ã Mehrdad Negahban and the University of Nebraska, 1996-2000.

All rights reserved

Copy and distribute freely for personal use only

Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526

Last modified at: 9:36 AM, Wednesday, March 08, 2000