Mohr’s Circle

 

Mohr’s circle for plane stress:

 

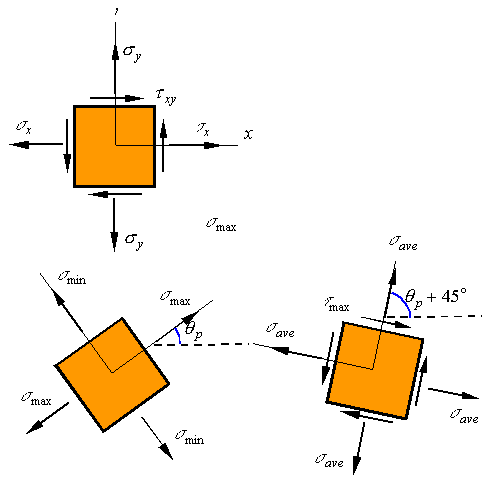
Consider the state of plane-stress shown in the figure.

 

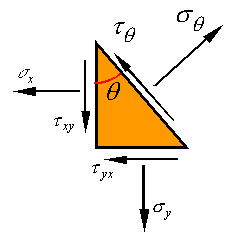
If negative the shear stress  is plotted against the normal stress  for each angle  of the incline, the resulting plot will be a circle of radius R and with its center located at . This can be directly shown by examining the equations for  and .

 

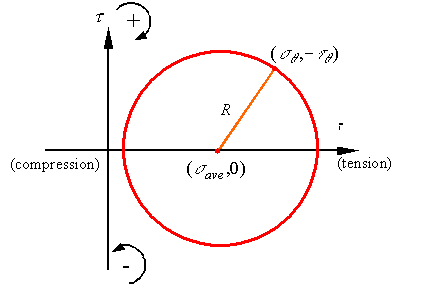
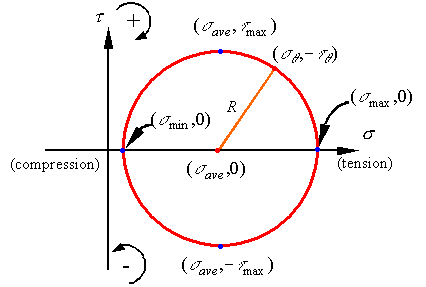
This circle is called Mohr’s circle and is a powerful tool for visualizing the possible states of stress at a material point. For example, at a glance one can see that the maximum normal stress at the point is the average stress plus the radius, the minimum normal stress at the point is the average stress minus the radius and the maximum shear stress at the point is equal to the radius.

 

 

The equations to calculate these stresses are

 

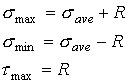
where

 

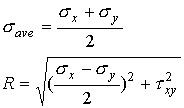
As can be seen the maximum and minimum normal stresses occur on surfaces that have zero shear stress, but the maximum shear stress occurs on a surface that has a normal stress equal to the average normal stress.

 

 

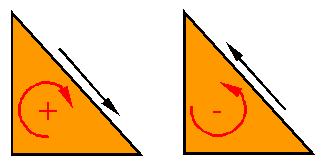
The convention for positive and negative shear stress on the Mohr’s circle is given on the axis and in terms of the direction of the shear stress on the stress element is shown in the following figure.

 

 

 

Locating points on Mohr’s circle:

 

One can locate points on Mohr’s circle by locating the point representing the surface normal to the x-axis, which has the coordinates , and then going along the circle an angle of  to get to the state of stress on the surface with an incline angle of .

 

 

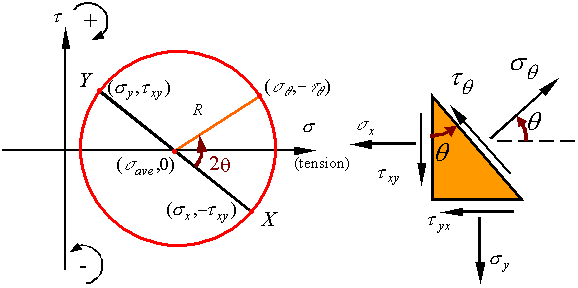
On Mohr’s circle, point  X represent the surface with normal along the x-direction and point Y represents the surface with normal along the y-direction. Since these surfaces are 90o apart on the stress element, on Mohr’s circle they are 180o apart (i.e., they end up on opposite sides of the circle). 

 

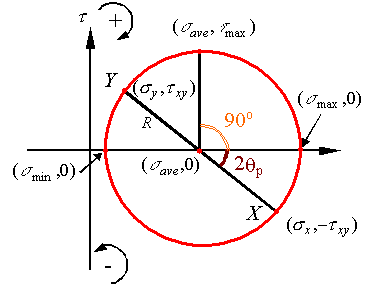
Principal stresses:

 

Principal stresses referrer to the maximum and minimum normal stresses. As can be seen on Mohr’s circle, the principal normal stresses occur on surfaces which have no shear stress. Also, the maximum shear stress is 90o away from the maximum normal stress on Mohr’s circle so that it is on a surface oriented 45o away from the surface on which the maximum normal stress occurs.

 

 

 

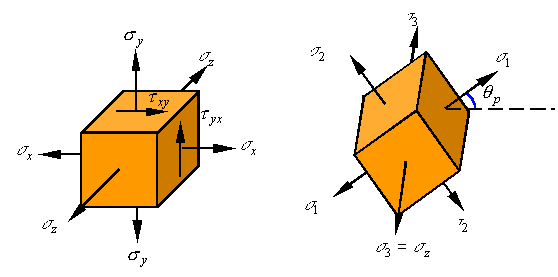
Out of plane stresses:

 

Consider the stress element shown where upon a state of plane stress a normal stress  is added in the third direction. Since this added stress is along a direction perpendicular to the plane stress, it does not interact with the in-plane stress (the stresses in the x-y plane) and all the results obtained for plane stress still hold. We can now rotate the stress element around the z-axis to get an element along the principal directions (only normal stresses remain).

 

Each two of the resulting directions now represents a simple state of plane stress for which shear stresses are zero. One can draw the three Mohr’s circles which result from each pair of directions to get the following Mohr’s circles. One can show that all states of stress fall between the three circles (the shaded area).

 

The absolute maximum and minimum normal stresses depend on the relative values of the three principal stresses , , and  (and need not be as shown in the figure). Also the maximum shear stress will equal the radius of the largest circle.

 

 


ã Mehrdad Negahban and the University of Nebraska, 1996-2000.

All rights reserved

Copy and distribute freely for personal use only

 

Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526

Last modified at: 9:42 AM, Monday, March 13, 2000