Pressure vessels
Spherical pressure vessels:
Consider
the stresses on one half of the thin spherical pressure vessel of inner radius r
and wall thickness t.
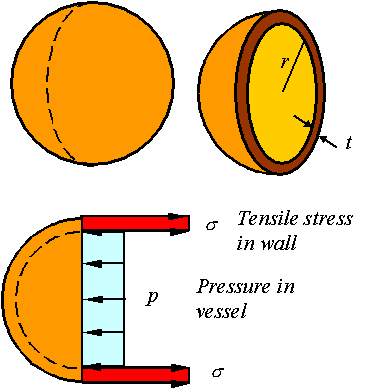
Static
equilibrium requires that the load generated from the tensile stress in the
wall be equal to the load applied by the pressure. Since the vessel is thin,
the load due to the tensile stress in the wall is ![]() . The load due to the pressure in the vessel is
. The load due to the pressure in the vessel is ![]() . Balancing these gives the expression for the stress in a
spherical vessel as
. Balancing these gives the expression for the stress in a
spherical vessel as
![]()
Due to symmetry in the spherical pressure vessel, the
stress in all directions tangent to the surface of the vessel is the same.
Depending on weather one takes a stress element from the inside or outside
surface of the vessel, one will get one of the two following states of stress.
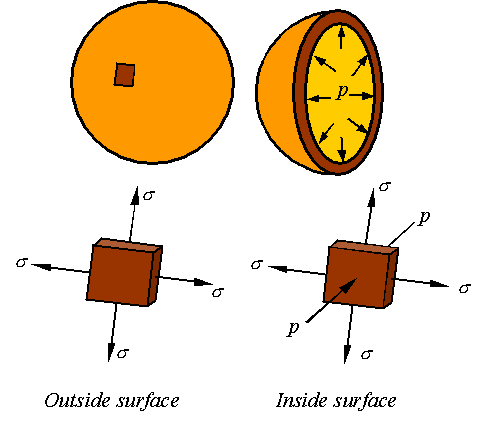
Maximum stress on the outside surface:
The
in and out-of-plane Mohrís circles for a stress element taken from the outside
surface of the pressure vessel will look as follows.
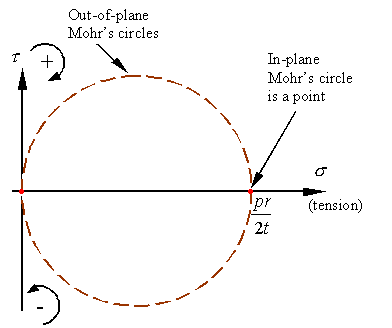
As
can be seen, the maximum and minimum normal stresses and maximum shear stress
are
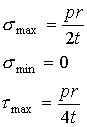
As
can also be seen, the maximum shear stress is on a 45o out-of-plane
incline as shown in the figure.
†

Maximum stress on the inside surface:
The
in and out-of-plane Mohrís circles for a stress element taken from the inside
surface of the pressure vessel will look as follows.
As
can be seen, the maximum and minimum normal stresses and maximum shear stress
are
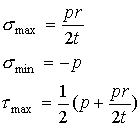
The
maximum shear stress is on a 45o out-of-plane inclined surface as
shown in the figure.
†

Cylindrical pressure vessels:
Consider
the stresses in a thin cylindrical pressure vessel of inner radius r and
wall thickness t.
Unlike
the spherical pressure vessel for which the stress in all directions tangent to
the sphere were the same, for a cylindrical pressure vessel the stress ![]() †along the axial
direction is different from the stress
†along the axial
direction is different from the stress ![]() †along the hoop
direction.
†along the hoop
direction.
Axial stress:
To
calculate the axial stress consider the stresses on a cross section of the
cylinder as shown in the figure.
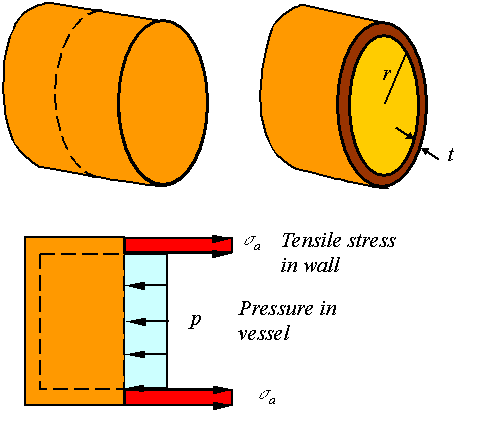
Static
equilibrium requires that the load generated from the tensile stress in the
wall to be equal to the load applied by the pressure. Since the vessel is thin,
the load due to the tensile stress in the wall is ![]() . The load due to the pressure in the vessel is
. The load due to the pressure in the vessel is ![]() . Balancing these gives the expression for the stress in a
spherical vessel as
. Balancing these gives the expression for the stress in a
spherical vessel as
![]()
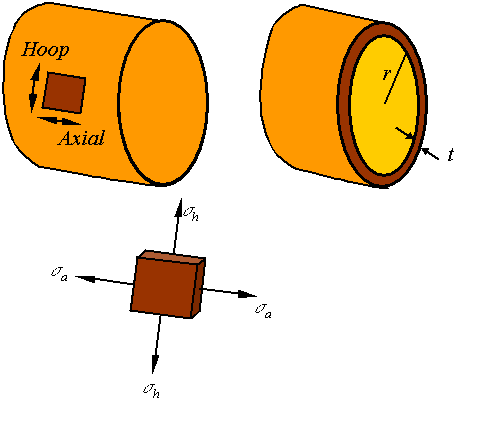
Hoop stress:
To
calculate the hoop stress consider the stresses on a section of the cylinder as
shown in the figure.
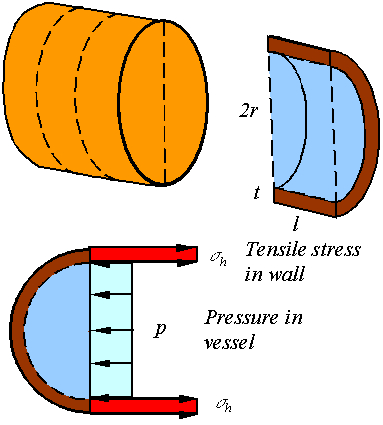
Static
equilibrium requires that the load generated from the tensile stress in the
wall to be equal to the load applied by the pressure. The load due to the
tensile stress in the wall is ![]() . The load due to the pressure in the vessel is
. The load due to the pressure in the vessel is ![]() . Balancing these gives the expression for the stress in a
spherical vessel as
. Balancing these gives the expression for the stress in a
spherical vessel as
![]()
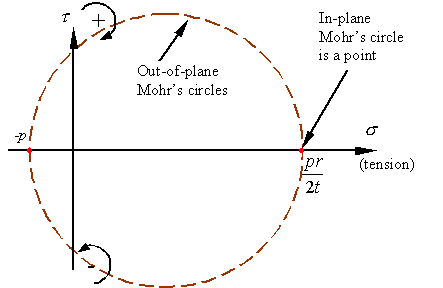
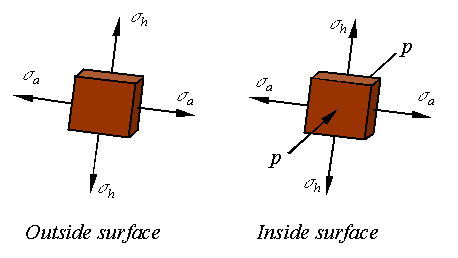
Maximum stresses on the inside and outside surface:
The
stress elements taken from the inside and outside surfaces of the cylindrical
pressure vessel look as follows.
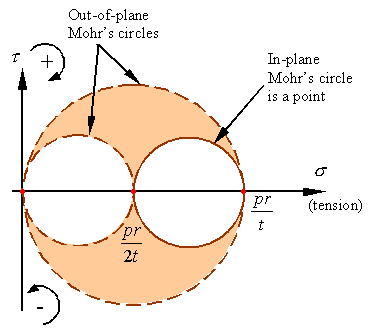
The in and out-of-plane Mohrís circles for a stress
element taken from the outside surface of the pressure vessel will look as
follows.
As
can be seen, the maximum and minimum normal stresses and maximum shear stress
are
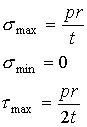
The
Mohrís circles for an element from inside the pressure vessel will look as
follows.

†
As
can be seen, the maximum and minimum normal stresses and maximum shear stress
on the inner surface of the vessel is given by
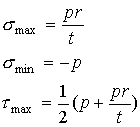
The
maximum shear stress is on the inner surface of the vessel and oriented on a surface
that is 45o out of plane (similar to the spherical vessel).
![]()
„ Mehrdad Negahban and the University of Nebraska, 1996-2000.
All rights reserved
Copy and distribute freely for personal use only
Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526
Last modified at: 10:32
AM,
Wednesday, March 15, 2000