Beam Deflection

 

Curvature of a line:

 

 

The radius of curvature , which is the radius of the circle that best “fits” a line at a given point, is the reciprocal of the curvature  of the line. From calculus we know that the curvature  of a line described by the function y = f(x) is given by the relation

 

 

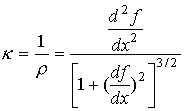
The beam deflection equation:

 

 

A beam under load deflects and bends. As shown in the figure, if the deflection of the beam is given by the displacement function v in terms of location x, from calculus we conclude that the curvature  of the beam is given

 

 

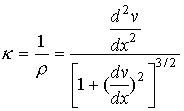
If the slope  of the curve describing the loaded beam is at all points small relative to unity then  and one can set the denominator of the expression for curvature equal to one. As a result, one obtains the approximate relation

 

 

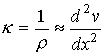
From the study of pure bending we know the relation between the radius of curvature and the applied bending moment to be given by the expression

 

 

Combining the relation for curvature from calculus and that obtained from mechanics of materials yields the beam equation:

 

 

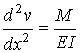
As the derivation implies, the beam equation in this form only hold for beams that at all points have small slope angles. This restriction can be removed by avoiding the approximation and using the full expression for curvature, but this not necessary for many applications that result in only small changes in the shape of the beam.

 

Uniform beams:

 

For beams with constant EI, one can easily differentiate the beam equation twice to get

 

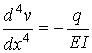
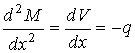This follows from the relations  and  that was obtained when we studied the shear and bending moment in beams. This expression can be integrated four times to get displacement v as a function of position x. The resulting expression will contain four constants of integration that are evaluated from imposing four boundary conditions. In general the process follows the following sequence:

 

 

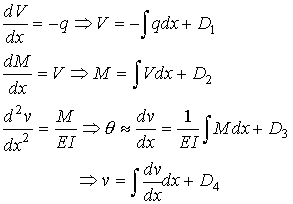
The four constants of integration are D1, D2, D3, and D4.

 

Example 1:

 

As an example, let us evaluate the deflection of a cantilevered beam of length l loaded by the application of a uniform load qo.

 

 

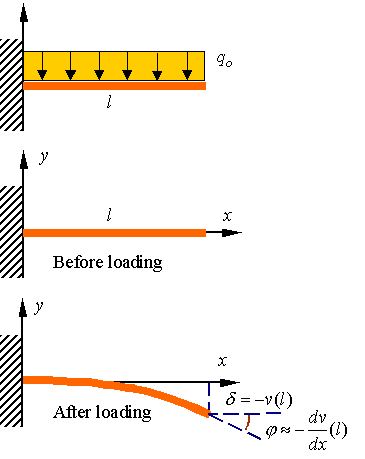
The equations are

 

 

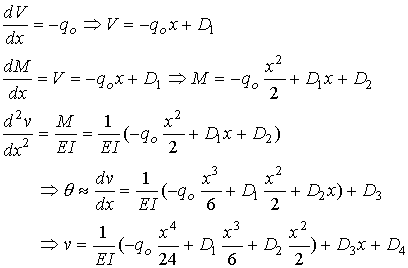
The boundary conditions on this beam are as follows. The slope and displacement at the left end must be zero since the support does not allow this end to move or rotate. The shear force and bending moment must be zero at the right end since it is free.

 

These boundary conditions require that

 

 

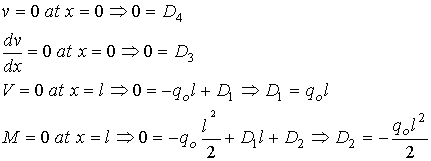
Therefore, the equations for the beam become

 

 

The slope and deflection at the right end is given by

 

 

The support reactions at the left end can directly be calculated from the equations for the shear and bending moments by substituting zero for the value of x. This results in

 

 

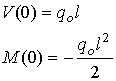
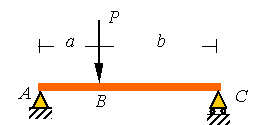
Example 2: A beam with two segments

 

In the following simply supported beam we look at a beam that has two segments (from A to B and from B to C), on each the segments the functions are continuous but the shear load has a jump due to the point load P when you go from one segment to the other. As a result one has different constants of integration for each segment.

 

 

Since the distributed load is equal to zero in both segments of the beam, the equations will be the similar up to the values of the integration constants. The equations for the first  segment are as follows.

 

From A to B (0<x<a):

 

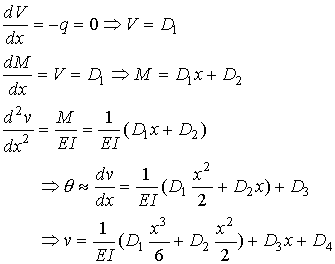
The equations are similar in the second segment, up to the integration constants. These equations are as follows.

 

From B to C (a<x<a+b):

 

 

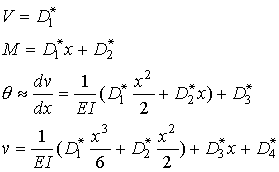
The boundary conditions at the two ends are as shown in the figure. As can be seen, the supports at the two ends impose a zero displacement condition and since the ends are free to rotate, the moment at each end is also zero. In addition to these four boundary conditions there are four continuity conditions at point B.

 

 

In addition to these four boundary conditions there are four continuity conditions at point B. Due to the point load, the shear load will have a jump at this point, but the other three variable do not change. All together, we will have eight conditions that will be used to solve for the eight constants of integration. These conditions are as follows, where l = a+b.

 

 

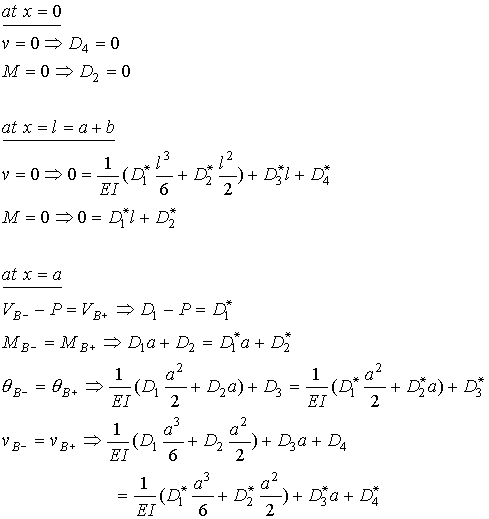
Once the eight constants Di and Di* are determined from these eight conditions, back substitution into the above equations gives the equations for the deflection of the beam in each of the two regions.

 

Example 3: Statically indeterminate beams

 

Consider the cantilever beam of the first example now propped up using a support at the right end. An examination of the free-body-diagram of the beam immediately indicates that the beam is statically indeterminate since we have four unknown support reactions and can only write three equilibrium equations.

 

 

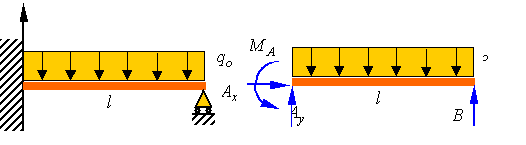
Since the distributed load on the beam is the same as in the first example, the equations for this beam will be similar to the first problem, but with different constants of integration. The equations are therefore given by the following set.

 

 

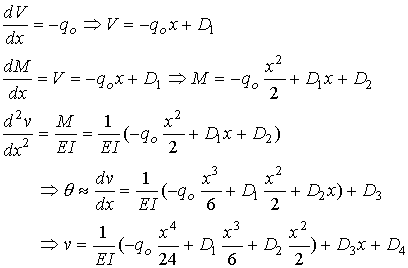
The boundary conditions for the left end are the same as the first example, but the boundary conditions on the right end require zero displacement and zero moment.

 

 

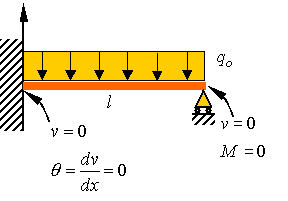
These four constraints are written as follows.

 

 

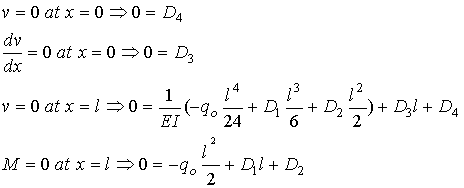
Solving these equations for the unknown constants of integration gives the following relations.

 

 

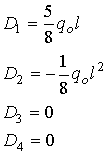
Substitution back into the original equations gives the following four equations for the beam.

 

 

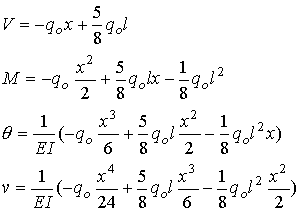
The support reactions can be calculated from the following relations.

 

 

 


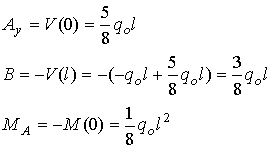
ã Mehrdad Negahban and the University of Nebraska, 1996-2000.

All rights reserved

Copy and distribute freely for personal use only

 

Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526

Last modified at: 5:41 PM, Thursday, April 13, 2000