Beam deflection by superposition of
solutions
Basic idea:
Since the beam deflection equation is linear, any
combination of solutions to this equation is itself a solution to the beam
equation. By adding known solutions of the beam equation together, one can
construct new solutions to the beam equation. In this way one can construct a
variety of solutions to fit a large number of boundary conditions. Tables of
solutions to the beam deflection equation can be found in most textbooks.
The key issue in construction of solutions using the method of superposition is that one select a set of knows solutions that in combination can satisfy the boundary conditions of the problem under consideration. Clearly this method is only useful when we can find solutions that when combined are capable of satisfying the boundary conditions of the problem under consideration.
Example:
Consider
the propped up cantilever beam show in the figure.
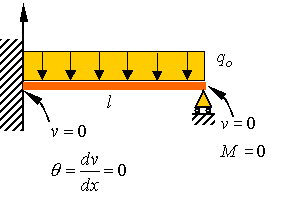
The
boundary conditions for this problem are indicated on the figure above. One can
consider this problem as the summation of the two problems shown in the figure
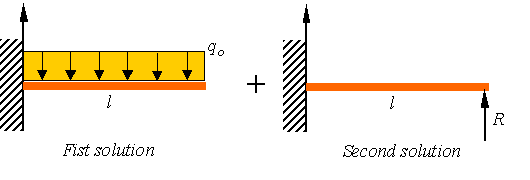
Clearly both solutions satisfy the zero displacement and
zero slop condition at the left side. Both solution satisfy the zero moment
condition on the right side. We simply need to make the combined solution
satisfy the zero displacement solution at the right tend of the beam. This can
be done by selecting the reaction force R in the second solution large
enough so that the combined solution does has zero displacement at the right
side of the bar. For the first solution the deflection downward of the right
end is given by
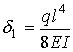
For
the second solution the deflection downward is given by
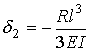
To
satisfy the zero displacement condition at the right end in the original
problem, we set the total displacement equal to zero and solve for the support
reaction R. That is
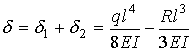
This yields the unknown reaction force at the right support as
![]()
The
solutions for the upward displacement of for each solution is given as
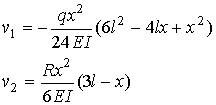
Combining the two solutions and substituting for the
support reaction yields the solution to the propped up cantilever as
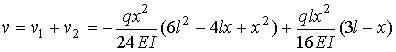
![]()
ã Mehrdad Negahban and the University of Nebraska, 1996-2000.
All rights reserved
Copy and distribute freely for personal use only
Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526
Last modified at: 6:45
PM,
Monday, November 20, 2000