Buckling of Columns

 

Basic idea:

 

Consider a column that is constructed from two pin-connected links with a torsional spring connected between the two links as shown in the figure. As long as the two bars AB and BC are perfectly aligned, the system is in equilibrium and one theoretically can increase the load until the beams fail in compression.

 

 

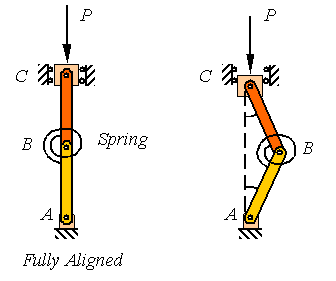
In reality, the two members can never be perfectly aligned so the system supports the load by the aid of the torsional spring and takes a shape such as shown in the right figure above.

 

Since the member ABC is a two-force member, the loads applied at A and C must be equal and along the line connecting A to C as shown in the above left figure. The free-body-diagram of AB shown on the right side of the figure above indicates that for equilibrium to hold, the miss-alignment angle  must increase until the moment in the torsional spring increases to balance the couple developed by the two vertical forces. This requires that

 

 

where kT is the stiffness of the torsional spring and the reader notes that the torsional spring is twisted twice the miss-alignment angle . Assuming small miss-alignment angles so that one can replace  by , one gets

 

 

Obviously,  is a solution to this equation. This solution represents the trivial solution that reflects the perfectly aligned system. But, this system has a non-trivial solution where the term in the parenthesis becomes zero to require

 

The load calculated in this way is called the critical load, designated by the subscript “cr”. For loads smaller than the critical load, the system will have accelerations that are consistent with bringing the system back into alignment. For loads above this critical load the system has accelerations consistent with increasing the miss-alignment angle, resulting in the collapse of the system. Therefore, the system is considered to be capable of carrying loads up to the critical load.

 

 

Buckling in a simply supported column:

 

Consider the pin-connected column AB of length L as shown in the following figure. Similar to the example above, if the column is fully aligned, the applied compressive load P can be increased until one reaches the compressive strength of the material. Yet, in reality the column will fail due to buckling as shown in the figure on the right long before this load is reached.

 

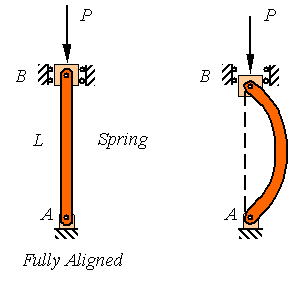
The analysis of the buckling of a continuous column is similar to the example given above to motivate the problem. Since the column is a two-force member, the reaction loads at the two pins are equal and directed along the line connecting the two pins as shown in the figure to the left below. The free-body-diagram of a segment of the column is also drown below and it is clear from this diagram that for the member to be in equilibrium the bending moment must balance the couple created by the misalignment of the two loads.

 

 

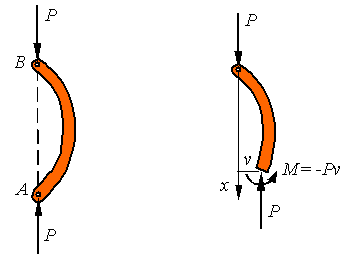
Designating the out of plane displacement of the column by v, the bending moment must be M=-Pv. One can combine this with the beam deflection equation

 

 

to get the equation for the column as

 

 

This is a second order homogeneous ordinary differential equation with constant coefficients that has a solution of the form

 

 

where C1 and C2 are constants to be fit to the boundary conditions and  must be restricted to satisfy the differential equation. The boundary conditions for this pin-supported column are that the displacement is zero at both supports. Therefore,

 

 

Obviously, if both C1 and C2 are zero one obtains the trivial solution v=0 for the fully aligned beam. For the beam to have a nontrivial solution (buckled solution), one must select  that results in requirement that  that yield

 

 

for any integer n. This results in the solution

 

 

As can be seen from the figure, different values of n represent different modes of buckling.

 

 

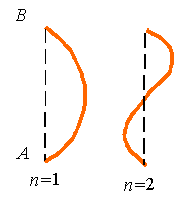
In addition to the boundary conditions, the solution must satisfy the differential equation. Substitution of this solution into the differential equation gives

 

 

Reorganization yields

 

 

Clearly, if C1 is zero, one arrives at the trivial solution v=0 that satisfies the differential equation, and which is associated with the fully aligned beam, but there is a non-trivial solution when the term in the round parentheses goes to zero. Therefore, to get a nontrivial solution to the buckling problem, the axial load must satisfy the relation

, which results in the expression for the critical load given by

 

 

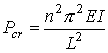
Obviously, the smallest critical load is associated with n=1. Therefore, the column will buckle at the load associated with the first buckling mode if the column is not restricted from taking the shape associated with this mode.

 

Different supports:

 

The buckling of columns with a variety of different support conditions are shown in the following figure and can be analyzed using similar procedures to the simply supported column studied above.

 

 

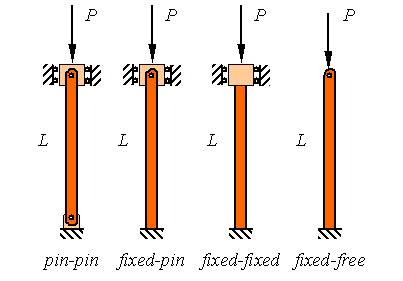
The results for the other columns are similar to the pin-pin supported column analyzed above with only the replacement of the actual length of the column with an effective length. If L is the actual length of the column and Le is the effective length of the column, then the critical buckling load for the column is given by

 

 

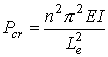
where the effective length Le is given by

 

 

 

 


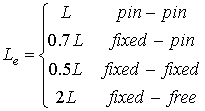
ã Mehrdad Negahban and the University of Nebraska, 1996-2000.

All rights reserved

Copy and distribute freely for personal use only

 

Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526

Last modified at: 5:32 PM, Monday, November 27, 2000