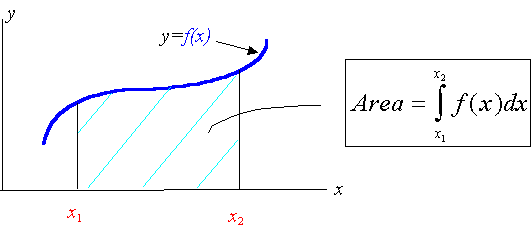
Integral of a function: The integral of a function f(x) over an interval from x₁ to x₂ yield the area under the curve in this interval

Note: The integral represents the as .

Note: Remember to add a constant of integration if you are not specifying limits. You evaluate the constant of integration by forcing the integral to pass through a known point.

Note: For definite integrals subtract the value of the integral at the lower limit from its value at the upper limit. For example, if you have the indefinite integral

where C is the constant of integration which drops out of the final expression.

Note: The following notation is common

Centroid of an area: The centroid of an area is the area weighted average location of the given area.