Equilibrium
of rigid bodies
Static
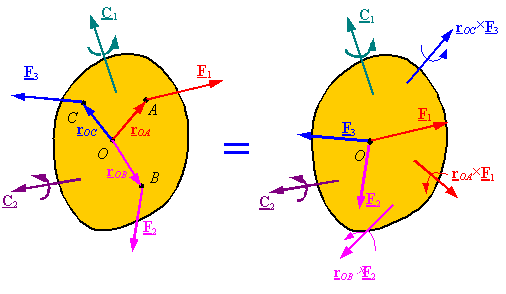
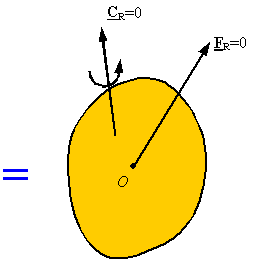
equilibrium for a rigid body: A body (or any part of it) which is currently
stationary will remain stationary if the resultant force and resultant moment
are zero for all the forces and couples applied
on it.
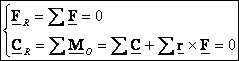
Free-Body
Diagram: A diagram
of a body (or a part of it) which shows all the forces and couples applied on
it, and which has all the forces and couples labeled for use in the solution of
the problem is called a free-body diagram. Follow these steps to draw a
free-body diagram.
1.
Select the body (or† part of a body) that you want to
analyze, and draw it.
2.
Identify all the forces and couples that are
applied onto the body and draw them on the body. Place each force and couple at
the point that it is applied.
3.
Label all the forces and couples with unique
labels for use during the solution process.
4.
Add any relevant dimensions onto your picture.
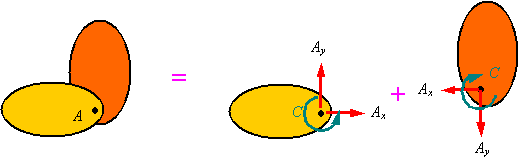
Composite bodies
and internal forces:† Forces and couples which are
a result of interaction between one part of an object and another part of it
will not appear in the free-body diagram of the whole object.
This is due to
Forces and
couples on a free-body diagram: Each force or couple you put on a free-body diagram
represents a model of how the body in the free-body diagram is effected by its surroundings. In selecting the forces and
couples that are to be applied on the free-body diagram follow these steps:
1.
Identify all the
forces which come from the interaction of one body with another. Many of the
common supports and their effects are shown in Table 5-1 on page 184. Remember
that for each way in which a support restricts the free motion of the body, a
force or a moment must be applied to the body to impose the restriction on the
motion.
2.
Apply the weight
of the body to its center of gravity (if it is uniform, then apply it to the centroid).
3.
Remember that
strings and cables can only pull on an object.
4.
Remember that
internal loads cancel out and should not be put on the free-body diagram.
5.
Remember that if
you have selected the direction of forces or couples of interaction on one
body, then
†
Solving for
unknowns: You
can write one set of equilibrium equations for each free-body diagram you draw. Things to remember are:
1.
In 2-D problems the
equilibrium equations result in three independent scalar equations (two components of force and
one component of moment). Therefore, you can only solve for three scalar
unknowns.
2.
Try to select the
point you take moments around such that the line of action of at least one
unknown force passes through that point. This will eliminate one unknown from
your moment equation and will result in simpler equations to work with. This
step is not essential, but will significantly simplify the algebra involved in
solving your system of equations.
3.
You can
sometimes take moments about two or three different points in a problem. Select
each point so that you eliminate one or more unknowns from the resulting moment
equation. Remember that the additional equations you generate in this way are
not independent of the original equations, and, therefore, you will still have only three independent equations in 2-D
problems per free-body diagram and you can
only solve for three unknowns per free-body diagram.
4.
For a composite
body, if you have drawn a free-body diagram and written the equilibrium
equations for each of its subsections, you will gain no additional information
if you draw the free-body diagram of the entire composite body and write its
equilibrium equations.
5.
In 3-D problems the
equilibrium equations result in six independent scalar equations (three components of force
and three components of moment). Therefore, you can solve for up to six scalar
unknowns per free-body diagram.
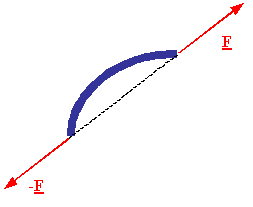
A two-force
member: A
body which has forces†
applied onto it at only two points, and no couples applied onto
it at all, is called a two-force member. A two-force member can only be in
equilibrium if the line of action of the resultant of the forces at each point
passes through the other point, and each resultant force is equal in magnitude
but opposite in direction to the resultant of the forces applied to the other
point.
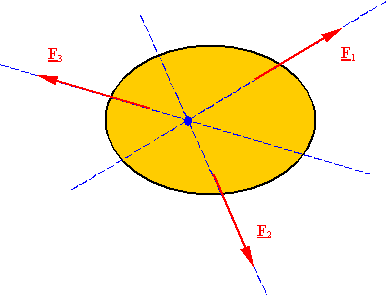
A three-force
member: A body
which has forces†
applied onto it at only three points, and no couples applied onto
it at all, is called a three-force member. A three-force member can only be in
equilibrium if the lines of action for the resultants of the forces at each
point intersect at a single point.
![]()
„ Mehrdad Negahban and the University of Nebraska, 1996-2000.
All rights reserved
Copy and distribute freely for personal use only
Department of Engineering Mechanics,