Shear Load and Bending Moment Diagrams
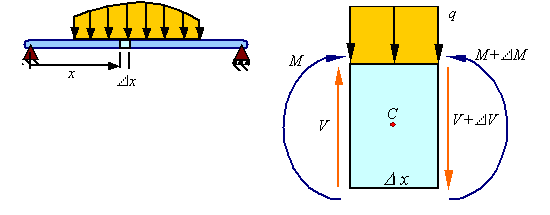
Equilibrium of forces: The
equilibrium of forces in the vertical direction in the segment shown of the
member results in
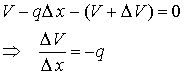
Taking the limit as ![]() gives
gives
![]()
Therefore, for continuous shear
loads, the change in shear is related to the integral of the distributed load.
Equilibrium of moments: The
equilibrium of moments around the centroid C
for the section shown yields
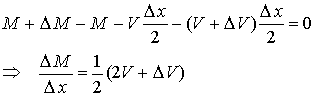
Taking the limit as ![]() gives
gives
![]()
Therefore, for continuous
moments, the change in moment is
related to the integral of the shear load (the area under the shear diagram is
related to the change in moment).
Point loads and point moments: When there is a point load Fo and a point
moment Mo applied at a point in the beam, the point load
results in a jump in the value of the shear load V and the point moment
results in a jump in the value of the bending moment M.
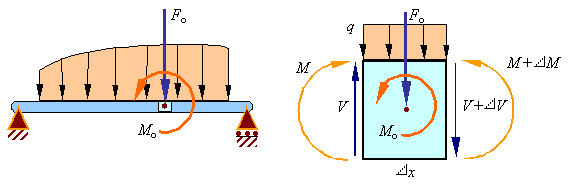
Equilibrium of forces on the
element requires that
![]()
Taking a limit as Dx goes to zero results
in the relation for the jump in the shear load due to an applied downward point
load of Fo to be given by
![]()
Equilibrium of moments on the
element requires that
![]()
Taking a limit as Dx goes to zero results
in the relation for the jump in the bending moment due to an applied
counter-clockwise point moment of Mo to be given by
![]()
Therefore, there will be a discontinuity at each applied point load in the shear diagram and a discontinuity at each applied couple in the moment diagram.
Drawing shear force and bending moment diagrams: The shear load and bending moment diagrams are constructed by integrating the distributed load to get the shear diagram (adding jumps at all point loads), and integrating the shear diagram to get the bending moment (adding jumps at all point couples). The following is an example of one shear load and bending moment diagram.
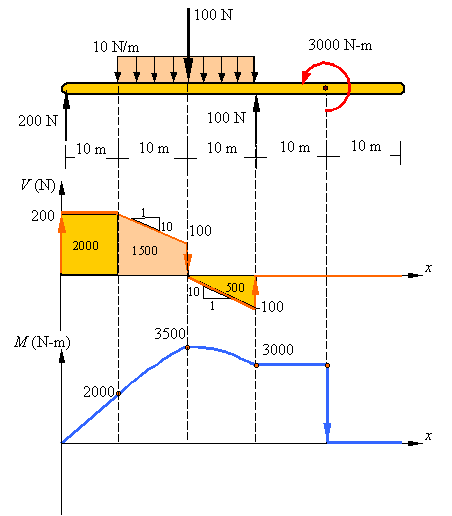
Note:
1. First draw the free-body-diagram of the beam with sufficient room under it for the shear and moment diagrams (if needed, solve for support reactions first).
2. Draw the shear diagram under the free-body-diagram. The distributed load is the slope of the shear diagram and each point load represents a jump in the shear diagram. Label all the loads on the shear diagram
3. Draw the moment diagram below the shear diagram. The shear load is the slope of the moment and point moments result in jumps in the moment diagram. The area under the shear diagram equals the change in moment over the segment considered (up to any jumps due to point moments). Label the value of the moment at all important points on the moment diagram.
![]()
ã Mehrdad Negahban and the
University of Nebraska, 1996-2000.
All
rights reserved
Copy
and distribute freely for personal use only
Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526