Shear Stress in Beams
Consider a segment of the beam shown. The shear load on the vertical surfaces are generated by shear stress that can be calculated by the following process.
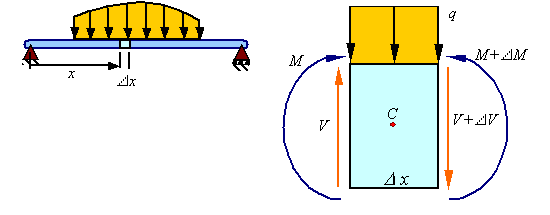
To calculate the shear stress t generated from the shear load V consider removing the segment of the beam shown in red.
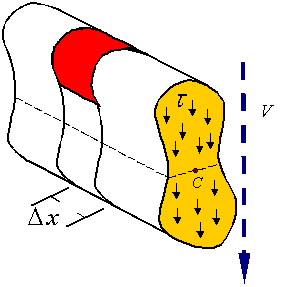
By symmetry of stress, shear stresses on the cross section results in equal shear stresses on the plane perpendicular to the cross section as shown. This shear stress results in a shear load Fs.

The side view of this segment, showing only axial loads, will look as follows
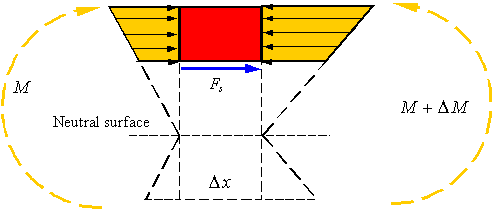
As can be seen, the difference in the bending moment on the two sides of the segment results in the normal stresses being different. The shear load Fs is the element that brings the segment into equilibrium. The axial load due to the normal stresses created by the bending moment can be calculated by integrating the normal stress over the area A* of the cross section.
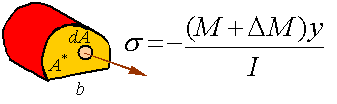
Therefore, equilibrium in the axial direction for this segment is written as
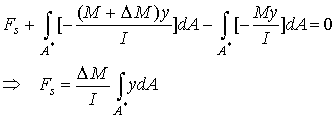
The integral in this expression is the first moment of the area A* about the neutral axis. This first moment will be denoted by Q so that

The shear stress can now be calculated from the shear load by dividing it by the area it is applied on to get
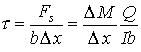
Taking the limit as ![]() gives
gives
![]()
where we note that ![]()
Calculating the first moment of the area: The first moment of the area can be calculated from the
relation
![]()
where A* is the area of the part of the
cross section that is considered, ![]() is the vertical
distance from the centroid of the cross section to the centroid of A*.
is the vertical
distance from the centroid of the cross section to the centroid of A*.

For composite areas, the first moment of area can be calculated for each part and then added together. The equation for Q in this case is
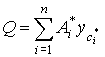
Shear stress along a slanted direction: The procedure presented does not require that the segment be cut with a surface parallel to the neutral surface. Therefore, one can remove a segment with the lower surface being at an oblique angle to the neutral surface so that the cross section will look as shown.
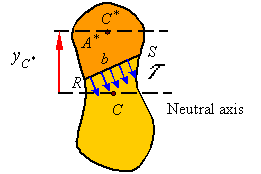
The shear calculated in this way is the average shear stress perpendicular to the line RS of width b.
![]()
ã Mehrdad Negahban and the
University of Nebraska, 1996-2000.
All
rights reserved
Copy
and distribute freely for personal use only
Department
of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526
Last modified at: 10:40 AM, Thursday, March 02, 2000