PURE SHEAR and POWER TRANSMISSION
Pure shear: Consider the material element loaded in pure shear as shown in the
figure
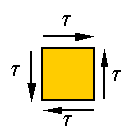
Stress
on an inclined plane in this element is neither pure shear nor pure tension, it
is a combination of both. Let ![]() and
and ![]() denote, respectively,
the shear and normal stresses on the surface that makes an angle
denote, respectively,
the shear and normal stresses on the surface that makes an angle ![]() with the vertical, as
shown in the following figure.
with the vertical, as
shown in the following figure.

One
can use equilibrium to calculate these stresses. If the area of the inclined
surface is A, then the area of the
vertical surface will be ![]() and the area of the
horizontal surface will be
and the area of the
horizontal surface will be ![]() , as shown in the above figure. The load on each surface can
be calculated using the stresses and the areas they are applied on. Therefore,
the free-body-diagram can be drawn as follows.
, as shown in the above figure. The load on each surface can
be calculated using the stresses and the areas they are applied on. Therefore,
the free-body-diagram can be drawn as follows.
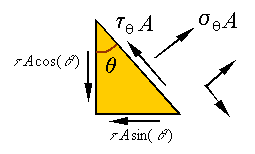
The
sum of forces along the incline yields
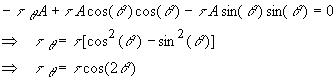
The
sum of forces along the normal to the incline yields

As
can be seen from these equations, the maximum shear
stress is ![]() and occurs when
and occurs when ![]() or in other words
when
or in other words
when

Note
that these surfaces are the original vertical and horizontal surfaces on which
the pure shear was applied. The maximum normal stress
is ![]() and occurs when
and occurs when ![]() or in other words
when
or in other words
when
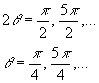
The
minimum normal stress is ![]() and occurs when
and occurs when ![]() or in other words
when
or in other words
when
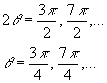
Note
that the maximum and minimum normal stresses occur on surfaces which are 90o
from one and other, and which are 45o from the vertical and
horizontal lines. Also, note that the shear stress is zero at the angles where
we have the maximum and minimum normal stresses. One can draw this on a diagram
representing the stress on an element that is cut from the original as follows
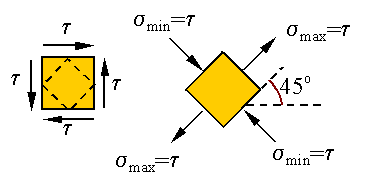
Since
in torsion material elements that have sides that are along and perpendicular
to the axis of the bar are subjected to pure shear, we can conclude that the
surfaces of maximum tensile stress scribes a 45o helix as shown below.
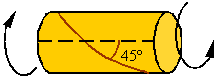
Ductile
materials fail in shear and, therefore, a shaft made from a ductile material
and under torsion will have a break surface that is perpendicular to the axis
of the bar. Brittle materials fail in tension and, therefore, a shaft made of a
brittle material and under torsion will break on a surface that is in the shape
of a 45o helix as shown above.
Strain in pure
shear:
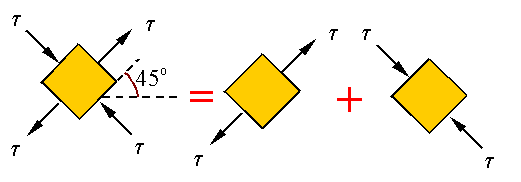
As
shown above, the state of stress described as pure shear can be replaced by a
state of stress that is a combination of tension and compression as follows
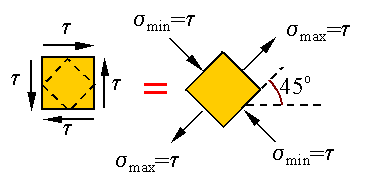
Let
us consider a linear elastic material. Since the theory is linear, we can
consider the following equivalence
Therefore,
the strains can be calculated based on the superposition of those resulting
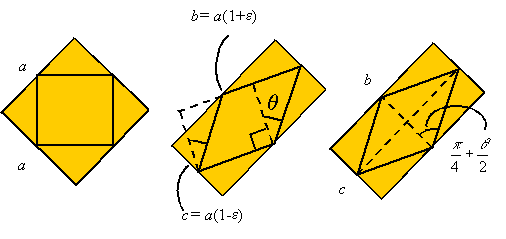
from the tension and compression. If the square originally has sides of length a, then we will have

where we have used Hooke's law ![]() for calculating the stretch along the axis of the load in
each of the uniaxial extensions and we have used Poisson's ratio to calculate
the transverse strain. Let us now look at how the shear and extension are
related. Take e to denote the total axial
strain given by
for calculating the stretch along the axis of the load in
each of the uniaxial extensions and we have used Poisson's ratio to calculate
the transverse strain. Let us now look at how the shear and extension are
related. Take e to denote the total axial
strain given by
![]()
The
following figure shows the deformation of both the original pure shear element
and the 45o element. In this figure q gives the angle of shear
which for small strains is approximately equal to the shear strain g.
From
the figure we can see that
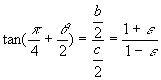
We
can expand the tangent function using the identity

Assuming
small angle q, we get the

For
small angles we know that ![]() , so that we get
, so that we get
![]()
This
relation can be used to relate the shear modulus to the elastic modulus and
Poisson ratio since we can substitute e from above into the
equation and use Hooke's law for shear to get
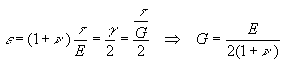
Note
that this expression states that the shear modulus, the elastic modulus, and
Poisson's ratio are not independent. One can calculate the third given any two.
Transmission of
power:
Power
is the rate at which work is being done. If P
denotes power and W denotes work,
then the relation between power and work can be written as
![]()
The
torque T applied on a shaft rotating
with an angular velocity w has a power given by the
expression
![]()
In
this expression the angular velocity is in radians per
unit time. The angular velocity is related to the frequency f by the relation
![]()
Therefore,
one can write
![]()
Power
can be given in terms of horsepower by the expression
![]()
where
n is in rpm (rounds per minute) and T is in lb-ft.
The
work done by a constant torque over a given
time interval can be calculated by integrating the power to get
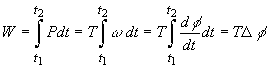
In
this expression ![]() is the total angle of
rotation over the given time interval.
is the total angle of
rotation over the given time interval.
ã Mehrdad Negahban and the University of Nebraska, 1996-2000.
All rights reserved
Copy and distribute freely for personal use only
Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526