TRIGONOMETRY FOR STATICS
PART 2:
The Unit
Circle and Visualizing Trigonometric Functions:
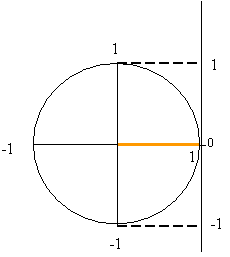
The fundamental relation 
suggests that the sine and cosine can be
visualized by using a circle of unit radius. To do this, draw a circle of unit
radius, as shown in the figure. Next draw a radial line from the center of the
circle to the its arc and making a counter clockwise angle 
with the horizontal
axis as shown in the figure. The projection of this line onto the horizontal
axis is 
, the projection of this line onto the vertical axis is 
, and if the
radial line is extended to intersect the vertical line AB one can get
as shown in
the figure.
From the unit circle one immediately discovers that the sine and cosine
functions can have values from -1 to 1, and that the tangent can have any value
form 
to
.
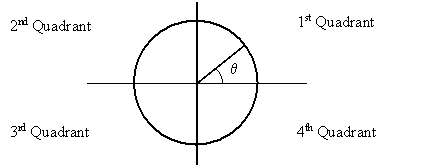
One denotes the quadrants of the unit circle as shown in the figure. It can be seen that the sine has positive value in the first and second quadrants, and negative value in the third and fourth quadrants. The cosine has positive value in the first and fourth quadrant and negative value in the second and third quadrants. The tangent has positive value in the first and third quadrants and negative value in the second and fourth quadrants.
The unit circle can also help one memorize the values of the trigonometric
functions. For example, at 
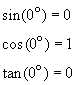
At 
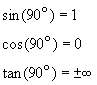
At 
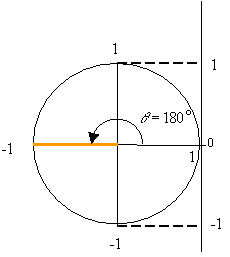
At 
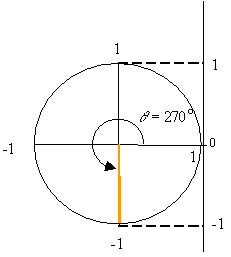
Inverse of
Trigonometric Functions:
The inverse trigonometric functions are: arcsine, arccosine, and
arctangent. For a specific value z, these are written as: 
, 
, 
. For
example, the function 
provides the angles 
that has 
. In a similar
manner, and , respectively, provide the angles for which 
and 
.
For example, 
means the angle for which the sine has a value of 0.5. Thus,
one solution is 
. Likewise, 
has a solution
.
The inverse trigonometric functions are also written as sin-1,
cos-1, and tan-1. For example, 
is the same as 
. This contradicts
the convention established for positive exponents. Therefore, even though 
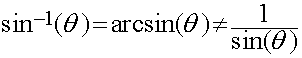
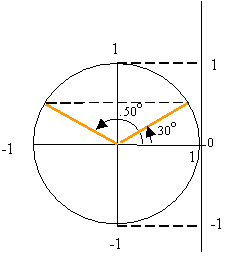
The inverse trigonometric functions are multi
valued. For example, the angles 
all satisfy the relation 
and are,
therefore, the solutions to . This can clearly be seen on the unit circle
since the projection of radial lines at 30o and 150o onto
the vertical axis are the same.
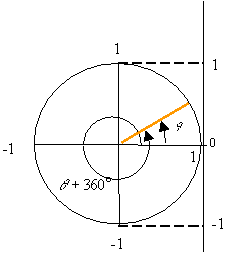
On the unit circle the addition of 360o to any angle results in a
new radial line that falls on top of the original radial line. Therefore, the
value of any trigonometric functions at an angle is the same as its value at 
. This is
also true for the addition of any integer multiple of 360o so that,
for example, 
for any integer n.
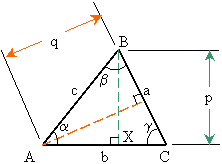
The law of sines states that
This can be shown by considering the triangles AXB and CXB in the
following figure. We have 
and 
, hence
or 
. In a similar manner one can show that 
.
The law of cosines states that
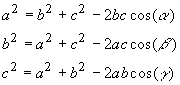
This can be shown by considering the triangle BXC that gives:
a2 = p2 + (CX )2 = p2 + (b - AX)2
or a2 = p2 + b2 + (AX)2 - 2b(AX)
(1)
Considering the triangle AXB one gets:
p2 + (AX)2 = c2 and 
Substituting these into (1) one obtains:
The other relations are obtained in a similar manner.