TRIGONOMETRY

Areas of focus:

1. Degrees versus radians
2. Trigonometric functions
3. Trigonometric relations between complementary angles
4. Pythagorean Theorem
5. The fundamental relation between sine and cosine
6. The unit circle and visualizing the trigonometric functions
7. Inverse of trigonometric functions
8. Law of sines
9. Law of cosines
10. Values of trigonometric at specific angles
11. Trigonometric identities
12. Curves of sine, cosine, and tangent
13. Approximation for small angles: sine, cosine, and tangent

Degrees Versus Radians:

One revolution is 360^o, and is also 2 radians. Thus, due to linear proportionality of the two scales, the conversion from x degrees to y radians is:

One radian is equal to 3.14159..., and is normally approximated by 3.14. The following table gives equivalent angles in degrees, radians, and revolutions.

Degrees	Radians	Revolutions
0^o	0	0
30^o
45^o
60^o
90^o
180^o
270^o
360^o		1

Trigonometric Functions:

The trigonometric functions are named sine, cosine, tangent, cotangent, secant, and cosecant. A trigonometric function has one argument that is an angle and will be denoted "". In writing the trigonometric functions one uses the abbreviated forms: , , , , , and , respectively. Also, sometimes these are written as , , , , , and , respectively.

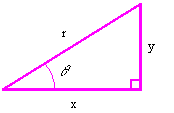
The value of each trigonometric function for an acute angle (<90^o) can be directly related to the sides of a right triangle. Consider the angle in the following figure. The values of the trigonometric functions for this angle are given as:

Note: the exponents of trigonometric functions follow a special rule. If the exponent "n" is positive, then one writes in place of . For example,

The same rule does not apply to negative exponents since the exponent "-1" is reserved for the inverse trigonometric function.

Functions of Complementary Angles:

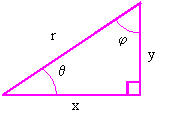
In this figure, and are complementary angles, meaning . Examination of the basic relation between the trigonometric functions and the sides of the triangle reveal the following relations between the complementary angles and.

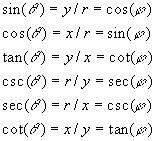
Since , we can also write:

Pythagorean Theorem:

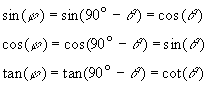
The Pythagorean theorem states that for a right triangle, as shown, there exists a relation between the length of the sides given be

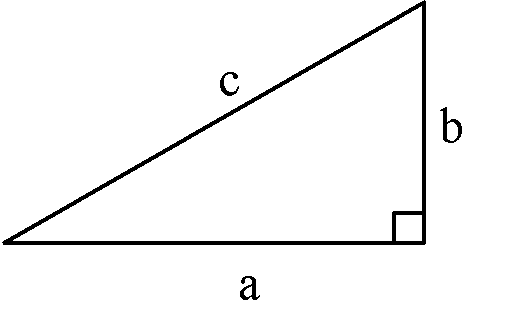
a² + b² = c²

There are also Pythagorean triples for (a,b,c), such as (3,4,5), (5,12,13) and (7,24,25) sided triangles, and all constant multiples of these triplets (e.g., (6,8,10)).

Fundamental Relations Among Trigonometric Functions:

From the Pythagorean Theorem of plane geometry we know that x² + y² = r². This can be used to derive a basic relation between the sine and cosine functions.

GO TO PART 2