TRIGONOMETRY FOR STATICS
PART 2:
The Unit
Circle and Visualizing Trigonometric Functions:
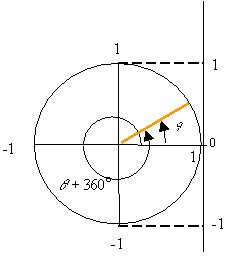
The fundamental relation ![]() suggests that the sine and cosine can be
visualized by using a circle of unit radius. To do this, draw a circle of unit
radius, as shown in the figure. Next draw a radial line from the center of the
circle to the its arc and making a counter clockwise angle
suggests that the sine and cosine can be
visualized by using a circle of unit radius. To do this, draw a circle of unit
radius, as shown in the figure. Next draw a radial line from the center of the
circle to the its arc and making a counter clockwise angle ![]() with the horizontal
axis as shown in the figure. The projection of this line onto the horizontal
axis is
with the horizontal
axis as shown in the figure. The projection of this line onto the horizontal
axis is ![]() , the projection of this line onto the vertical axis is
, the projection of this line onto the vertical axis is ![]() , and if the
radial line is extended to intersect the vertical line AB one can get
, and if the
radial line is extended to intersect the vertical line AB one can get![]() as shown in
the figure.
as shown in
the figure.
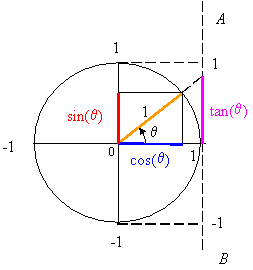
From the unit circle one immediately discovers that the sine and cosine
functions can have values from -1 to 1, and that the tangent can have any value
form ![]() to
to
![]() .
.
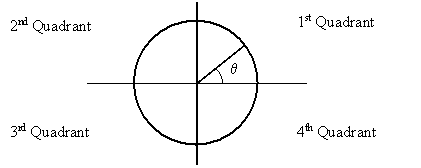
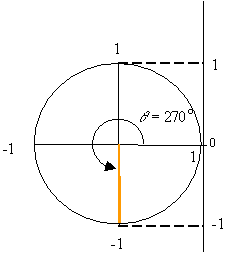
One denotes the quadrants of the unit circle as shown in the figure. It can be seen that the sine has positive value in the first and second quadrants, and negative value in the third and fourth quadrants. The cosine has positive value in the first and fourth quadrant and negative value in the second and third quadrants. The tangent has positive value in the first and third quadrants and negative value in the second and fourth quadrants.
The unit circle can also help one memorize the values of the trigonometric
functions. For example, at ![]()
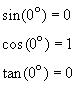
At ![]()
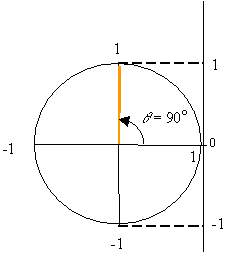
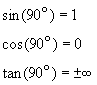
At ![]()
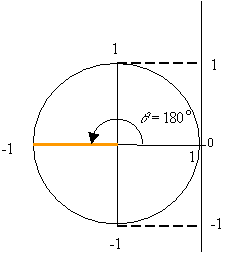
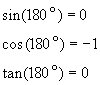
At ![]()
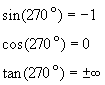
Inverse of
Trigonometric Functions:
The inverse trigonometric functions are: arcsine, arccosine, and
arctangent. For a specific value z, these are written as: ![]() ,
, ![]() ,
, ![]() . For
example, the function
. For
example, the function ![]() provides the angles
provides the angles ![]() that has
that has ![]() . In a similar
manner,
. In a similar
manner, ![]() and
and ![]() , respectively, provide the angles for which
, respectively, provide the angles for which ![]() and
and ![]() .
.
For example, ![]() means the angle
means the angle ![]() for which the sine has a value of 0.5. Thus,
one solution is
for which the sine has a value of 0.5. Thus,
one solution is ![]() . Likewise,
. Likewise, ![]() has a solution
has a solution![]() .
.
The inverse trigonometric functions are also written as sin-1,
cos-1, and tan-1. For example, ![]() is the same as
is the same as ![]() . This contradicts
the convention established for positive exponents. Therefore, even though
. This contradicts
the convention established for positive exponents. Therefore, even though ![]()
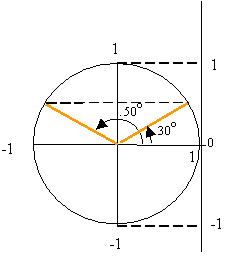
The inverse trigonometric functions are multi
valued. For example, the angles ![]() all satisfy the relation
all satisfy the relation ![]() and are,
therefore, the solutions to
and are,
therefore, the solutions to ![]() . This can clearly be seen on the unit circle
since the projection of radial lines at 30o and 150o onto
the vertical axis are the same.
. This can clearly be seen on the unit circle
since the projection of radial lines at 30o and 150o onto
the vertical axis are the same.
![]()
On the unit circle the addition of 360o to any angle results in a
new radial line that falls on top of the original radial line. Therefore, the
value of any trigonometric functions at an angle ![]() is the same as its value at
is the same as its value at ![]() . This is
also true for the addition of any integer multiple of 360o so that,
for example,
. This is
also true for the addition of any integer multiple of 360o so that,
for example, ![]() for any integer n.
for any integer n.
The law of sines states that
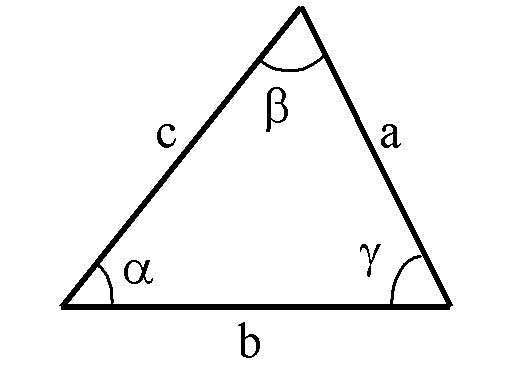
![]()
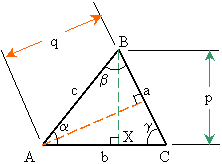
This can be shown by considering the triangles AXB and CXB in the
following figure. We have ![]() and
and ![]() , hence
, hence![]() or
or ![]() . In a similar manner one can show that
. In a similar manner one can show that ![]() .
.
The law of cosines states that

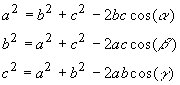
This can be shown by considering the triangle BXC that gives:

a2 = p2 + (CX )2 = p2 + (b - AX)2
or a2 = p2 + b2 + (AX)2 - 2b(AX)
(1)
Considering the triangle AXB one gets:
p2 + (AX)2 = c2 and ![]()
Substituting these into (1) one obtains:
![]()
The other relations are obtained in a similar manner.