Dynamic Analysis

The dynamics portion attemps to find when the structure will break. Using guesses for how much tension and compression each member can take, it gradually increases the force until a beam snaps. The applet version uses a value slightly higher than the maximum applied load for the strengths of the members, whereas the application version includes this data inside file inputs.

A dynamic load is simply one that changes. When a truss is analyzed straight-forward, all the dynamic loads are taken at their maximum values. When a truss is dynamically analyzed, however, each dynamic load is set to the same ratio of their maximums; ie, all dynamic loads are at 12% or 79% at the same time.

The method used to find when a truss breaks involves a simple binary search. First, the limits are checked: if the truss is already broken at 0% of the dynamic loads (all static loads) or doesn't have any broken members at 100%, then there's no point in going further, and the search is cancelled. If not, then the truss is analyzed at the midway point between the maximum and minimum loads. If the truss is broken at the midway point, then the midpoint becomes the new maximum, and the search continues; otherwise, the midpoint becomes the new minimum value.

Using a binary search is much more efficient than stepping through values until a break is found. To get an accuracy of +/- 0.005%, you would need 1/.00005, or some 2000 steps, to find the breaking point. Using a binary search, you would only need some ln(1/.00005)/ln(2), or 11 steps to get the same accuracy. (The binary search gets closer by a factor of 2 each time, so by the 11th step it has covered 2^11 or 2048 load ranges.) The truss analysis module was programmed to step through 15 iterations, or some 32000 load ranges. While this is not necessary, the Gaussian REF algorithm is fast enough that this is no problem, and gives an accuracy of +/- 0.003%, if needed.

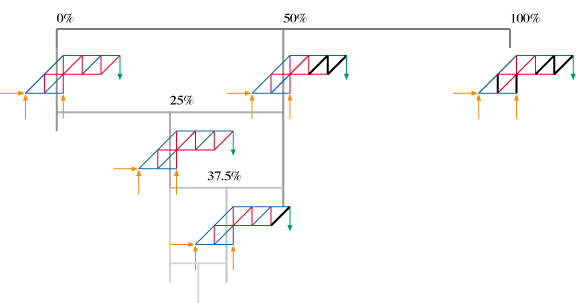
An example of a three step (row) binary search