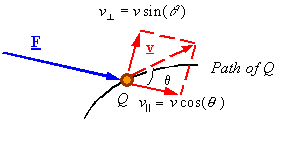The work-energy relation
Power of a force:
Power in
the ability of a force to do work
![]()
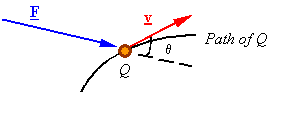
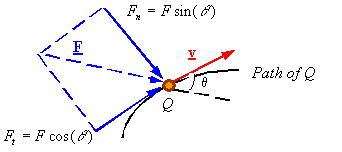
F: The force applied on
particle Q
|
|
v: The velocity of Q
Note: The power of a force
is related to the velocity of the particle it is acting upon.
|
|
![]()
|
|
Work of a force: The work U1-2 of
a force on a particle over the interval of time from
t1 to t2 is the integral of its power over this time
interval.
|
|

Other
methods to find the work of a force are:
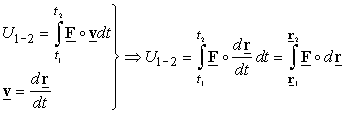
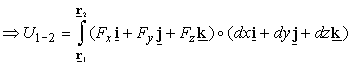
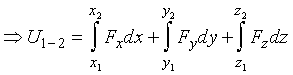

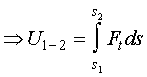
Kinetic energy of
a particle: A
particle of mass m at each instant in
time has a kinetic energy T given by
![]()
The work-energy
relation:
The relation between the work done on a particle by the forces which are
applied on it and how its kinetic energy changes follows from Newton’s second
law.
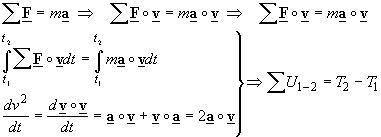
Note:
The work done on a particle by the resultant force applied on it over a given
interval of time will be equal to the change in kinetic energy of the particle.
In other words, the kinetic energy of a particle is changed by an amount equal
to the work which is done on the particle by the resultant force.
![]()
![]()
ã Mehrdad Negahban and the
University of Nebraska, 1999-2002.
All
rights reserved
Copy
and distribute freely for personal use only
Department of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526