Potential Energy
Conservative
forces: A
force F is conservative if it
can be represented as the gradient of a scalar function. This can written as
![]()
where
V is a scalar function of position in
space. The negative sign is only for convenience so that V can be identified as the potential energy.
Work of a
conservative force: Given a conservative force F, its work can be calculated as
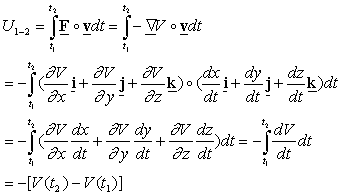
Therefore,
the work of a conservative force is negative the change in its potential
energy.
Note: Since the work of a
conservative force does not depend on the path the particle takes when going
from its location at time 1 to its location at time 2, the
work of a conservative force is path independent.
The work-energy
relation: The work energy relation can
be rewritten to take advantage of the fact that you can calculate the work of
conservative forces form the potential energy. Let the resultant work of all
forces on a particle be separated into the work done by conservative forces and
the work done by non-conservative forces as follows
![]()
Introduction
of this into the work energy relation gives
![]()
![]()
Total Mechanical
Energy: The
total mechanical energy† E is the sum of the kinetic energy and
the potential energy of the conservative forces.
![]()
The
work energy relation can now be written as
![]()
Conservative
systems: A conservative system is one
for which the total mechanical energy E
remains constant. This can only happen if the non-conservative forces do no
work.
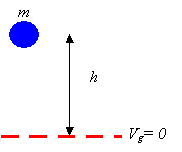
Potential energy
of gravity: The potential energy of
gravity is given by
![]()
where
h is measured from an elevation
selected as reference.
|
|
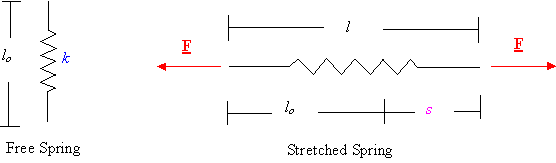
Potential energy
of a spring: The
potential energy of a spring is given by
![]()
where
k is the spring stiffness, l is the springís current length, and lo is the free length of the
spring, and s is the stretch of the
spring.
|
|
Example 3
![]()
„ Mehrdad Negahban and the
University of Nebraska, 2000.
All
rights reserved
Copy
and distribute freely for personal use only
Department
of Engineering Mechanics, University of Nebraska, Lincoln, NE 68588-0526